（本题12分）如图，四棱柱ABCD—A
BCD中，AD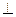
平面ABCD，底面ABCD是边长为1的正方形，侧棱AA=2．
（1）求证：CD∥平面ABBA；
（2）求直线BD与平面ACD所成角的正弦值；
（3）求二面角D—AC一A的余弦值．
推荐套卷
（本题12分）如图，四棱柱ABCD—ABCD中，AD平面ABCD，底面ABCD是边长为1的正方形，侧棱AA=2．
（1）求证：CD∥平面ABBA；
（2）求直线BD与平面ACD所成角的正弦值；
（3）求二面角D—AC一A的余弦值．
粤公网安备 44130202000953号