某中学在新课改活动中，成立了机器人小组，他们在一次实验中，要观察坐标平面内沿一正方形四周运动的质点，为了记录这个质点的任何时刻的运动数据和位置，特在垂直于坐标平面原点的正上方1个单位长度处安装一探测仪，它的探测范围是以自身为球心，半径可调节的球，现已知质点运动轨迹的正方形四个顶点为（0，0）、（1，0）、（1，1）、（0，1），那么探测仪的探测半径最少要调到 （ ）
| A．1 | B．2 | C． |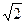
D． |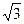
相关试题
在定义域上为
奇函数，则
（）
，若
对于任意实数x恒成立，则实数b的取值范围是（）
的所有集合B的个数是( )
( )推荐套卷
某中学在新课改活动中，成立了机器人小组，他们在一次实验中，要观察坐标平面内沿一正方形四周运动的质点，为了记录这个质点的任何时刻的运动数据和位置，特在垂直于坐标平面原点的正上方1个单位长度处安装一探测仪，它的探测范围是以自身为球心，半径可调节的球，现已知质点运动轨迹的正方形四个顶点为（0，0）、（1，0）、（1，1）、（0，1），那么探测仪的探测半径最少要调到 （ ）
| A．1 | B．2 | C． |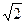
D． |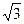
粤公网安备 44130202000953号