下面四个命题:
①在空间中,过直线外一点只能作一条直线与该直线平行;
②“直线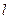 ⊥平面
⊥平面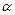 内所有直线”的充要条件是“
内所有直线”的充要条件是“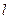 ⊥平面
⊥平面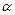 ”;
”;
③“平面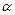 ∥平面
∥平面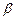 ”的必要不充分条件是“
”的必要不充分条件是“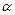 内存在不共线三点到
内存在不共线三点到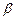 的距离相等”;
的距离相等”;
④若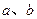 是异面直线,
是异面直线,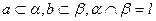 则
则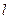 至少与
至少与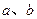 中的一条相交.
中的一条相交.
其中正确命题的个数有 ( )
| A.1 | B.2 | C.3 | D.4 |
推荐套卷
下面四个命题:
①在空间中,过直线外一点只能作一条直线与该直线平行;
②“直线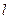 ⊥平面
⊥平面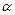 内所有直线”的充要条件是“
内所有直线”的充要条件是“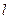 ⊥平面
⊥平面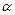 ”;
”;
③“平面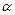 ∥平面
∥平面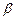 ”的必要不充分条件是“
”的必要不充分条件是“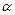 内存在不共线三点到
内存在不共线三点到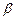 的距离相等”;
的距离相等”;
④若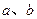 是异面直线,
是异面直线,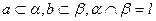 则
则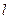 至少与
至少与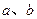 中的一条相交.
中的一条相交.
其中正确命题的个数有 ( )
| A.1 | B.2 | C.3 | D.4 |