选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
(1)(选修4—4坐标系与参数方程)已知直线的极坐标方程为 ,则极点到该直线的距离是 .
,则极点到该直线的距离是 .
(2)(选修4—5 不等式选讲)已知 ,则满足不等式
,则满足不等式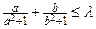 的实数
的实数 的范围
的范围 是 .
是 .
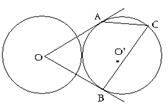
(3)(选修4—1 几何证明选讲)如图,两个等圆⊙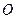 与⊙
与⊙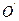 外切,过
外切,过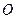 作⊙
作⊙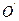
 的两条切线
的两条切线
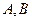 是切点,点
是切点,点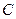 在圆
在圆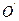 上且不与点
上且不与点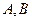 重合,则
重合,则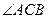 = .
= .
推荐套卷
选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
(1)(选修4—4坐标系与参数方程)已知直线的极坐标方程为 ,则极点到该直线的距离是 .
,则极点到该直线的距离是 .
(2)(选修4—5 不等式选讲)已知 ,则满足不等式
,则满足不等式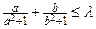 的实数
的实数 的范围
的范围 是 .
是 .
(3)(选修4—1 几何证明选讲)如图,两个等圆⊙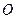 与⊙
与⊙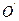 外切,过
外切,过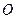 作⊙
作⊙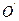
 的两条切线
的两条切线
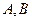 是切点,点
是切点,点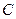 在圆
在圆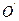 上且不与点
上且不与点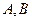 重合,则
重合,则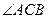 = .
= .