给出下列命题：
①函数
为非零常数）的图象可由函数y=3x的图象经过平移得到；
②函数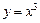
在R上既是奇函数又是增函数.
③不等式
④函数
至多有一个交点.
⑤若定义在R上的函数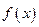
满足
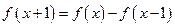,则函数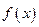是周期函数.
⑥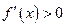
在定义域内恒成立函数
在定义域内单调递增的充分不必要条件.
其中正确命题的序号是 .（把你认为正确命题的序号都填上）
则
的最小值是 。
的前n项和为
，
成等差数列，则
等于 。
等于 。
三边及内部组成的区域为
，
，当点P在
的最大值为 。相关知识点
推荐套卷
给出下列命题：
①函数为非零常数）的图象可由函数y=3x的图象经过平移得到；
②函数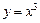在R上既是奇函数又是增函数.
③不等式
④函数至多有一个交点.
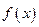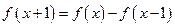⑤若定义在R上的函数满足,则函数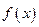是周期函数.
⑥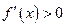在定义域内恒成立函数在定义域内单调递增的充分不必要条件.
其中正确命题的序号是 .（把你认为正确命题的序号都填上）
粤公网安备 44130202000953号