已知F1、F2是椭圆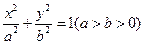
的左、右焦点，A是椭圆上位于第一象限内的一点，点B也在椭圆上，且满足
（
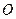是坐标原点），
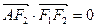,若椭圆的离心率等于
.
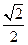（1）求直线AB的方程；
（2）若三角形ABF2的面积等于4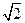
，求椭圆的方程；
（3）在（2）的条件下，椭圆上是否存在点M，使得三角形MAB的面积等于8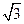
.
；
的图象在点P处的切线方程是
，则
化为十进制数，结果为__ _ 
，0)，则椭圆的标准方程是推荐套卷
已知F1、F2是椭圆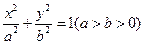的左、右焦点，A是椭圆上位于第一象限内的一点，点B也在椭圆上，且满足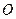（是坐标原点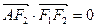），,若椭圆的离心率等于.
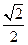（1）求直线AB的方程；
（2）若三角形ABF2的面积等于4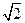，求椭圆的方程；
（3）在（2）的条件下，椭圆上是否存在点M，使得三角形MAB的面积等于8.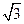
粤公网安备 44130202000953号