我们可以运用下面的原理解决一些相关图形的面积问题：如果与一固定直线平行的直线被甲、乙两个封闭图形所截得线段的比为定值
，那么甲的面积是乙的面积的倍，你可以从给出的简单图形①（甲：大矩形
、乙：小矩形
）、②（甲
：大直角三角形
乙：小直角三角形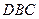
）中体会这个原理，现在图③中的曲线分别是
与
，运用上面的原理，图③中椭圆的面积为 ．
与直线
平行，则实数
的值为.
________
的最小正周期等于_______
，则a 与b的夹角为______推荐套卷
我们可以运用下面的原理解决一些相关图形的面积问题：如果与一固定直线平行的直线被甲、乙两个封闭图形所截得线段的比为定值，那么甲的面积是乙的面积的倍，你可以从给出的简单图形①（甲：大矩形、乙：小矩形）、②（甲：大直角三角形乙：小直角三角形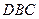）中体会这个原理，现在图③中的曲线分别是与，运用上面的原理，图③中椭圆的面积为 ．
粤公网安备 44130202000953号