(本小题满分13分)
随机抽取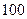 名学生,测得他们的身高(单位:
名学生,测得他们的身高(单位: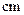 ),按照区间
),按照区间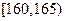 ,
,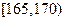 ,
,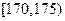 ,
,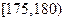 ,
,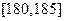 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).
(Ⅰ)求频率分布直方图中 的值及身高在
的值及身高在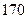
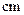 以上的学生人数;
以上的学生人数;
(Ⅱ)将身高在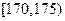 ,
,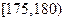 ,
,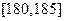 区间内的学生依次记为
区间内的学生依次记为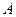 ,
,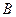 ,
,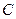 三个组,用分层抽样的方法从三个组中抽取
三个组,用分层抽样的方法从三个组中抽取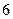 人,求从这三个组分别抽取的学生人数;
人,求从这三个组分别抽取的学生人数;
(Ⅲ)在(Ⅱ)的条件下,要从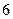 名学生中抽取
名学生中抽取 人,用列举法计算
人,用列举法计算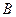 组中至少有
组中至少有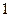 人被抽中的概率.
人被抽中的概率.
相关知识点
推荐套卷
(本小题满分13分)
随机抽取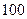 名学生,测得他们的身高(单位:
名学生,测得他们的身高(单位: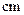 ),按照区间
),按照区间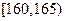 ,
,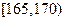 ,
,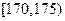 ,
,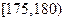 ,
,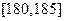 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).
(Ⅰ)求频率分布直方图中 的值及身高在
的值及身高在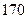
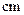 以上的学生人数;
以上的学生人数;
(Ⅱ)将身高在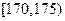 ,
,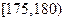 ,
,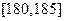 区间内的学生依次记为
区间内的学生依次记为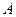 ,
,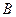 ,
,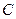 三个组,用分层抽样的方法从三个组中抽取
三个组,用分层抽样的方法从三个组中抽取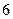 人,求从这三个组分别抽取的学生人数;
人,求从这三个组分别抽取的学生人数;
(Ⅲ)在(Ⅱ)的条件下,要从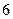 名学生中抽取
名学生中抽取 人,用列举法计算
人,用列举法计算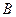 组中至少有
组中至少有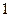 人被抽中的概率.
人被抽中的概率.