已知命题P: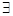 
x∈R,mx2+1≤0，命题q: 
x∈R,x2+mx+1＞0 ，若p∨q 为假命题，则实数m的取值范围为 （ ）
| A．m≤-2 | B．m≥2 |
| C．m≤-2或m≥2 | D．-2≤m≤ 2 |
的前n项和为
，若
，则
等于（ ）
中，
，则三角形的形状为（ ）
则
（ ）
中
，则
等于（ ）
的前n项和为
，且
=6，
=4， 则公差
等于（ ）
推荐套卷
已知命题P: 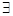x∈R,mx2+1≤0，命题q: x∈R,x2+mx+1＞0 ，若p∨q 为假命题，则实数m的取值范围为 （ ）
| A．m≤-2 | B．m≥2 |
| C．m≤-2或m≥2 | D．-2≤m≤ 2 |
粤公网安备 44130202000953号