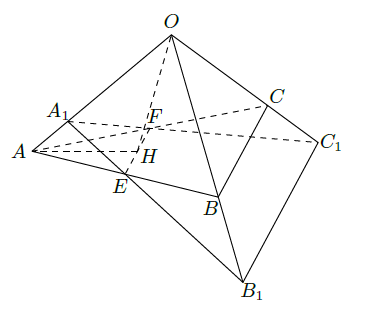
如图,正三棱锥
的三条侧棱
两两垂直,且长度均为2.
分别是
的中点,
是
的中点,过
作平面与侧棱
或其延长线分别相交于
,已知
。
(1)求证:
平面
;
(2)求二面角
的大小。
推荐套卷
如图,正三棱锥
的三条侧棱
两两垂直,且长度均为2.
分别是
的中点,
是
的中点,过
作平面与侧棱
或其延长线分别相交于
,已知
。

(1)求证:
平面
;
(2)求二面角
的大小。