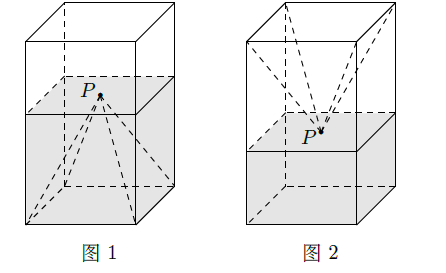
如图1，一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有 升水时，水面恰好经过正四棱锥的顶点 。如果将容器倒置，水面也恰好过点 （图2）。有下列四个命题：
| A． | 正四棱锥的高等于正四棱柱高的一半 |
| B． | 将容器侧面水平放置时，水面也恰好过点 |
| C． | 任意摆放该容器，当水面静止时，水面都恰好经过点 |
| D． | 若往容器内再注入 升水，则容器恰好能装满 |
其中真命题的代号是：
)＝
，则cos(
－2α)的值为
是定义在R上的奇函数，且当x＜0时，
则方程
有▲个实根．
，且
，则
的值为▲．
的偶函数
在
上为增函数，且
，则不等式
的解集为
▲．推荐套卷
如图1，一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有 升水时，水面恰好经过正四棱锥的顶点 。如果将容器倒置，水面也恰好过点 （图2）。有下列四个命题：
| A． | 正四棱锥的高等于正四棱柱高的一半 |
| B． | 将容器侧面水平放置时，水面也恰好过点 |
| C． | 任意摆放该容器，当水面静止时，水面都恰好经过点 |
| D． | 若往容器内再注入 升水，则容器恰好能装满 |
其中真命题的代号是：
粤公网安备 44130202000953号