(本题满分16分,第(1)小题6分,第(2)小题10分)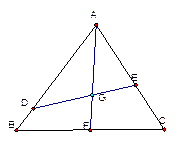
如图,已知点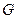 是边长为
是边长为 的正三角形
的正三角形 的中心,线段
的中心,线段 经过点
经过点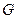 ,并绕点
,并绕点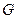 转动,分别交边
转动,分别交边 、
、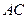 于点
于点 、
、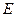 ;设
;设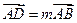 ,
,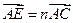 ,其中
,其中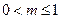 ,
,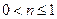 .
.
(1)求表达式 的值,并说明理由;
的值,并说明理由;
(2)求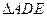 面积的最大和最小值,并指出相应的
面积的最大和最小值,并指出相应的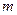 、
、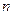 的值.
的值.
推荐套卷
(本题满分16分,第(1)小题6分,第(2)小题10分)
如图,已知点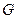 是边长为
是边长为 的正三角形
的正三角形 的中心,线段
的中心,线段 经过点
经过点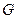 ,并绕点
,并绕点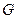 转动,分别交边
转动,分别交边 、
、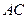 于点
于点 、
、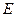 ;设
;设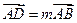 ,
,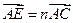 ,其中
,其中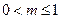 ,
,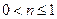 .
.
(1)求表达式 的值,并说明理由;
的值,并说明理由;
(2)求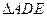 面积的最大和最小值,并指出相应的
面积的最大和最小值,并指出相应的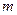 、
、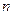 的值.
的值.