(本小题满分12分)已知函数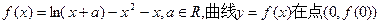 处的切线恰好为
处的切线恰好为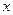 轴。(I)求
轴。(I)求 的值;(II)若区间
的值;(II)若区间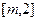 恒为函数
恒为函数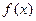 的一个单调区间,求实数
的一个单调区间,求实数 的最小值;(III)记
的最小值;(III)记 (其中
(其中 ),
), 的导函数,则函数
的导函数,则函数 是否存在极值点?若存在,请找出极值点并论证是极大值点还是极小值点;若不存在,请说明理由。
是否存在极值点?若存在,请找出极值点并论证是极大值点还是极小值点;若不存在,请说明理由。
推荐套卷
(本小题满分12分)已知函数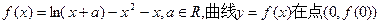 处的切线恰好为
处的切线恰好为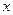 轴。(I)求
轴。(I)求 的值;(II)若区间
的值;(II)若区间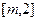 恒为函数
恒为函数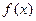 的一个单调区间,求实数
的一个单调区间,求实数 的最小值;(III)记
的最小值;(III)记 (其中
(其中 ),
), 的导函数,则函数
的导函数,则函数 是否存在极值点?若存在,请找出极值点并论证是极大值点还是极小值点;若不存在,请说明理由。
是否存在极值点?若存在,请找出极值点并论证是极大值点还是极小值点;若不存在,请说明理由。