若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线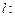
 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, (其中
(其中 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断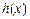 与
与 间的隔离直线方程为 .
间的隔离直线方程为 .
推荐套卷
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线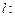
 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, (其中
(其中 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断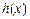 与
与 间的隔离直线方程为 .
间的隔离直线方程为 .