一根轻绳一端系一小球,另一端固定在O点,在O点有一个能测量绳的拉力大小的力传感器,让小球绕O点在竖直平面内做圆周运动,由传感器测出拉力F随时间t变化图像如图所示,已知小球在最低点A的速度vA=6m/s,求:
(1)小球做圆周运动的周期T;
(2)小球的质量m;
(3)轻绳的长度L;
(4)小球在最高点的动能Ek.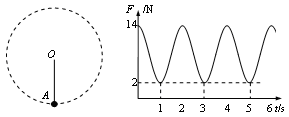
一根轻绳一端系一小球,另一端固定在O点,在O点有一个能测量绳的拉力大小的力传感器,让小球绕O点在竖直平面内做圆周运动,由传感器测出拉力F随时间t变化图像如图所示,已知小球在最低点A的速度vA=6m/s,求:
(1)小球做圆周运动的周期T;
(2)小球的质量m;
(3)轻绳的长度L;
(4)小球在最高点的动能Ek.