某工厂生产某种产品，已知该产品的月生产量x（t）与1 t产品的价格p（元/t）之间的关系为：p="24" 200-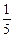
x2，且生产xt的成本为R（元），其中R="50" 000+200x.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入-成本）
和A∩C=
，求证：
推荐套卷
某工厂生产某种产品，已知该产品的月生产量x（t）与1 t产品的价格p（元/t）之间的关系为：p="24" 200-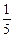x2，且生产xt的成本为R（元），其中R="50" 000+200x.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入-成本）
粤公网安备 44130202000953号