一条河的两岸平行，河的宽度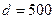
m，一艘船从
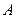处出发到河对岸．已知船的速度
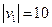km/h，水流速度
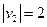km/h．要使船行驶的时间最短，那么船行驶的距离与合速度的比值必须最小．此时我们分三种情况讨论：
（１） 当船逆流行驶，与水流成钝角时；
（２） 当船顺流行驶，与水流成锐角时；
（３） 当船垂直于对岸行驶，与水流成直角时．
请同学们计算上面三种情况，是否当船垂直于对岸行驶时，与水流成直角时，所用时间最短
相关试题
，若不等式
的解集为
.
在C上有解，求实数
的取值范围.
满足
且对于任意
, 恒有
成立. （1）求实
数
的值; （2）解不等式
.
，其中
.
的最小
正周期和单调递增区间；
的取值范围。
＝(3,2)，
＝
(－1,2)，
＝(4,1)．(1)
求满足
(2
时, 证明: 不等式
恒成立; 
满足
,证明数列
是等比数列,并求出数列
，证明：
.推荐套卷
一条河的两岸平行，河的宽度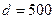m，一艘船从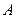处出发到河对岸．已知船的速度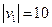km/h，水流速度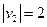km/h．要使船行驶的时间最短，那么船行驶的距离与合速度的比值必须最小．此时我们分三种情况讨论：
（１） 当船逆流行驶，与水流成钝角时；
（２） 当船顺流行驶，与水流成锐角时；
（３） 当船垂直于对岸行驶，与水流成直角时．
请同学们计算上面三种情况，是否当船垂直于对岸行驶时，与水流成直角时，所用时间最短
粤公网安备 44130202000953号