（本小题满分16分）某连锁分店销售某种商品，每件商品的成本为4元，并且每件商品需向总店交a元（1≤a≤3）的管理费，预计当每件商品的售价为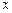
元（8≤x≤9）时，一年的销售量为(10－x)2万件．（1）求该连锁分店一年的利润L（万元）与每件商品的售价x的函数关系式L(x)；（2）当每件商品的售价为多少元时，该连锁分店一年的利润L最大，并求出L的最大值M(a)．
相关试题
的前
项和为
,且
.
满足
，求数列
．
对任意x∈R恒成立，求m的取值范围.
直线l和抛物线y2=2x相交于A、B两点，设线段AB的中点为M,求：(1)|PM|； (2)|AB|.
并有特征值λ2=-1及属于特征值-1的一个特征向量
(1)求矩阵M.(2)求M5α.
的前
项和为
，已知
(n∈N*)．
，数列
的前
项和为
．利用（2）的结论证明：当n∈N*且n≥2时，
.推荐套卷
（本小题满分16分）某连锁分店销售某种商品，每件商品的成本为4元，并且每件商品需向总店交a元（1≤a≤3）的管理费，预计当每件商品的售价为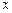元（8≤x≤9）时，一年的销售量为(10－x)2万件．（1）求该连锁分店一年的利润L（万元）与每件商品的售价x的函数关系式L(x)；（2）当每件商品的售价为多少元时，该连锁分店一年的利润L最大，并求出L的最大值M(a)．
粤公网安备 44130202000953号