如图△ABC为直角三角形，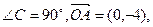
点M在y轴上，且
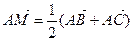，点C在x轴上移动，（I）求点B的轨迹E的方程；（II）过点
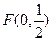的直线l与曲线E交于P、Q两点，
设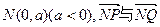
的夹角为
的取值范围； （III）设以点N(0，m)为圆心，以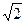
为
半径的圆与曲线E在第一象限的交点H，若圆在点H处的
切线与曲线E在点H处的切线互相垂直，求实数m的值。
反比例函数
，二次函数
的单调性。
是定义在区间
上的偶函数，命题
：
上单调递减；命题
：
，若“
或
的取值范围。
的图象全在
轴的上方成立的充要条件。
至少有一个负实根的充要条件。
：
方程
必有实根；
：
使得
。推荐套卷
如图△ABC为直角三角形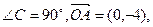，点M在y轴上，且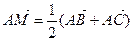，点C在x轴上移动，（I）求点B的轨迹E的方程；（II）过点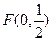的直线l与曲线E交于P、Q两点，
设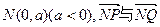的夹角为
的取值范围； （III）设以点N(0，m)为圆心，以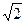为
半径的圆与曲线E在第一象限的交点H，若圆在点H处的
切线与曲线E在点H处的切线互相垂直，求实数m的值。
粤公网安备 44130202000953号