如图所示，光滑的曲面轨道的水平出口跟停在光滑水平面上的平板小车的上表面相平，质量为m的小滑块从光滑轨道上某处由静止开始滑下并滑下平板小车，使得小车在光滑水平面上滑动．已知小滑块从光滑轨道上高度为H的位置由静止开始滑下，最终停到板面上的Q点．若平板小车的质量为3m．用g表示本地的重力加速度大小，求：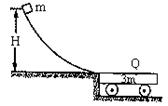
（1）小滑块到达轨道底端时的速度大小v0；
（2）小滑块滑上小车后，平板小车可达到的最大速度V；
（3）该过程系统产生的总热量Q．
相关试题
对某行星的一颗卫星进行观测，已知运行的轨迹是半径为r的圆周，周期为T，求：
（1）该行星的质量；
（2）测得行星的半径为卫星轨道半径的1/10，则此行星表面重力加速度为多大？
一物体在地球表面重
16N，将它挂在以a=5m/s2的加速度竖直上升的火箭中的弹簧秤钩上，弹簧秤示数F=9N，求此火箭离地球表面的距离为地球半径的几倍？（
m/s2）
粤公网安备 44130202000953号