（本小题满分12分）已知函数
(x>0)在x = 1处取得极值
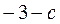，其中a,b,c为常数。
(1)试确定a,b的值； (2) 讨论函数f(x)的单调区间；
(3)若对任意x>0，不等式
恒成立，求c的取值范围。
相关试题
（本小题满分13分）在平面直角坐标系
中，已知椭圆
：
（
）的左焦点为
，且点
在上.
（Ⅰ）求椭圆的方程；
（Ⅱ）已知直线
的斜率为2且经过椭圆的左焦点.求直线与该椭圆相交的弦长。
，B=
， 
时，求
.
：
，
：
，且
的取值范围。
满足圆的标准方程
，
的最小值；
到圆上点的最大值.
.
时，求
的极值；
时，求
及
，恒有
成立，求
的取值范围
的公差大于0,且
是方程
的两根,数列
的前
项的和为
，且
．
,求证：
；
的前
．推荐套卷
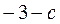（本小题满分12分）已知函数(x>0)在x = 1处取得极值，其中a,b,c为常数。
(1)试确定a,b的值； (2) 讨论函数f(x)的单调区间；
(3)若对任意x>0，不等式恒成立，求c的取值范围。
（本小题满分13分）在平面直角坐标系中，已知椭圆：（）的左焦点为，且点在上.
（Ⅰ）求椭圆的方程；
（Ⅱ）已知直线的斜率为2且经过椭圆的左焦点.求直线与该椭圆相交的弦长。
粤公网安备 44130202000953号