电磁炮是利用磁场对电流的作用力，把电能转变成机械能，使炮弹发射出去的.如图所示，把两根互相平行的长直铜制轨道放在磁场中，轨道之间搁有长为l、质量为M的金属架，金属架上安放质量为m的炮弹.当有电流I1通过轨道和金属架时，炮弹与金属架整个在磁场力的作用下，获得速度v1时刻的加速度为a；当有大的电流I2通过轨道和炮弹时，炮弹最终以最大速度v2脱离金属架并离开轨道，则垂直于轨道平面的磁感应强度B为多大？（设金属架与炮弹在运动过程中所受的总阻力与速度的平方成正比）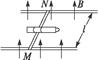
相关试题
(16分)一辆汽车沿平直公路从甲站开往乙站，启动加速度为2 m/s2，加速行驶5 s后匀速行驶2 min，然后刹车，滑行50 m，正好到达乙站，求汽车从甲站到乙站的平均速度为多少．
相关知识点
粤公网安备 44130202000953号