已知h>0，设命题甲为：两个实数a、b满足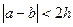
，命题乙为：两个实数a、b满足
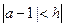且
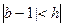，那么
| A．甲是乙的充分但不必要条件 | B．甲是乙的必要但不充分条件 |
| C．甲是乙的充要条件 | D．甲是乙的既不充分也不必要条件 |
= (cosθ, sinθ)，
= (
, 1)，则
的最大值为( )
的公比为正数，且
=2
，
=1，则
=（ ）
，
”的否定是（ ）
，
，则A∩B等于（ ）
相关知识点
推荐套卷
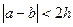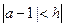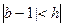已知h>0，设命题甲为：两个实数a、b满足，命题乙为：两个实数a、b满足且，那么
| A．甲是乙的充分但不必要条件 | B．甲是乙的必要但不充分条件 |
| C．甲是乙的充要条件 | D．甲是乙的既不充分也不必要条件 |
粤公网安备 44130202000953号