平面直角坐标系中,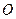 为坐标原点,给定两点
为坐标原点,给定两点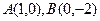 ,点
,点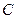 满足
满足 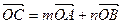 ,其中
,其中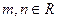 ,且
,且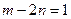 . (1)求点
. (1)求点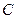 的轨迹方程;(2)设点
的轨迹方程;(2)设点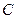 的轨迹与双曲线
的轨迹与双曲线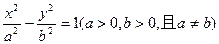 交于
交于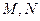 两点,且以
两点,且以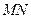 为直径的圆过原点,求证:
为直径的圆过原点,求证: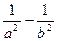 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于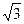 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
推荐套卷
平面直角坐标系中,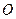 为坐标原点,给定两点
为坐标原点,给定两点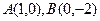 ,点
,点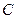 满足
满足 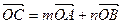 ,其中
,其中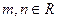 ,且
,且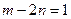 . (1)求点
. (1)求点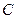 的轨迹方程;(2)设点
的轨迹方程;(2)设点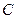 的轨迹与双曲线
的轨迹与双曲线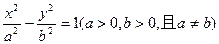 交于
交于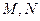 两点,且以
两点,且以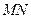 为直径的圆过原点,求证:
为直径的圆过原点,求证: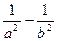 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于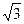 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.