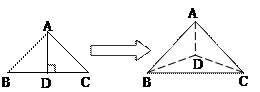
如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：
①
；
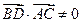②∠BAC＝60°；
③三棱锥D—ABC是正三棱锥；
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确的是 （ ）
| A．①② | B．②③ | C．③④ | D．①④ |
相关试题
+
=1上两点，F2为椭圆的右焦点，若|AF2|+|BF2|=
a，AB中点到椭圆左准线的距离为
，求该椭圆方程．
，短轴长为
，求椭圆的方程．
是椭圆
上的点，则
的取值范围是_______________ ．推荐套卷
如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：
①；
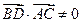②∠BAC＝60°；
③三棱锥D—ABC是正三棱锥；
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确的是 （ ）
| A．①② | B．②③ | C．③④ | D．①④ |
粤公网安备 44130202000953号