设是已知平面上所有向量的集合,对于映射,记的象为。若映射满足:对所有及任意实数都有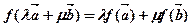 ,则称为平面上的线性变换。现有下列命题:
,则称为平面上的线性变换。现有下列命题:
①设是平面上的线性变换,则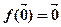
②对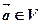 设
设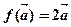 ,则是平面上的线性变换;
,则是平面上的线性变换;
③若是平面上的单位向量,对设,则是平面上的线性变换;
④设是平面上的线性变换,,若共线,则也共线。
其中真命题是(写出所有真命题的序号)
相关知识点
推荐套卷
设是已知平面上所有向量的集合,对于映射,记的象为。若映射满足:对所有及任意实数都有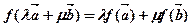 ,则称为平面上的线性变换。现有下列命题:
,则称为平面上的线性变换。现有下列命题:
①设是平面上的线性变换,则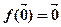
②对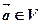 设
设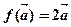 ,则是平面上的线性变换;
,则是平面上的线性变换;
③若是平面上的单位向量,对设,则是平面上的线性变换;
④设是平面上的线性变换,,若共线,则也共线。
其中真命题是(写出所有真命题的序号)