湖南省娄底市湘中名校九年级上学期第二次联考数学试卷
下列结论中正确的是( )
| A.两个正方形一定相似 | B.两个菱形一定相似 |
| C.两个等腰梯形一定相似 | D.两个直角梯形一定相似 |
下列条件不能判定△ABC与△A′B′C′相似的是( )
| A.∠C=∠C′=90°∠B=∠A′=50° |
B.∠A=∠A′=90° |
C.∠A=∠A′  |
D. |
如果两个相似三角形对应边的比是3:4,那么它们的对应高的比是( )
| A.9:16 | B. :2 :2 |
C.3:4 | D.3:7 |
已知,如图,DE∥BC,EF∥AB,则下列结论:
① ②
② ③
③ ④
④
其中正确的比例式的个数是( )
| A.4个 | B.3个 | C.2个 | D.1个 |

在△ABC与△DEF中,有下列条件:①AB:DE="BC:EF" ②BC:EF="AC:DF" ③∠B=∠E④∠C=∠F.如果从中任取两个条件组成一组,那么能判断△ABC与△DEF相似的共有( )
| A.2组 | B.3组 | C.4组 | D.5组 |
三角形三边之比3:5:7,与它相似的三角形最长边是21cm,另两边之和是( )。
| A.15cm | B.18cm | C.21cm | D.24cm |
在平面直角坐标系中,已知A(6,3),B(6,0)两点,以坐标原点O为位似中心,位似比为 ,把线段AB缩小到线段
,把线段AB缩小到线段 ,则
,则 的长度等于( )
的长度等于( )
| A.1 | B.2 | C.3 | D.6 |
在比例尺为1:m的某市地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是( )米2
A. |
B.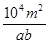 |
C.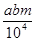 |
D.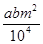 |
如图,P是Rt△ABC的斜边BC上异于B,C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )。
| A.1条 | B.2条 | C.3条 | D.4条 |
两个相似三角形面积之比是9:25,较大的三角形的周长是20cm,则较小的三角形的周长是______cm.
如图,∠DAB=∠CAE,请补充一个条件:______________,使△ABC ∽△ADE.
如图,测量小玻璃管口径的量具ABC,AB的长度为5mm,AC被分为50等份,如果小玻璃管口DE正好对着量具上30份处(DE∥AB),那么小玻璃管口径DE的长为________.
如图,点D是△ABC的边AB上的一点,AD=6,BD=2,当AC= 时,△ABC∽△ACD.
如图,在梯形ABCD中,AD∥BC,EF∥BC,若AD=12cm,BC=17cm,AE:EB=2:3,则EF=__________
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA’B’C’与矩形OABC关于点O位似,且矩形OA’B’C’的面积等于矩形OABC面积的 ,B的坐标是(6,4),那么点B’的坐标是
,B的坐标是(6,4),那么点B’的坐标是 
矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△ABE∽△DFA
(2)若AB=6,AD=12,AE=10,求DF的长
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′ C′的顶点都在格点上
(1)求证:△ABC∽△A′ B′ C′
(2)△A′ B′ C′与△ABC是位似图形吗?如果是,在图上画出位似中心并求出位似比
如图,已知菱形AMNP内接于△ABC,M、N、P分别在AB、BC、AC上,如果AB=21 cm,CA=15cm,求菱形AMNP的周长.
小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB长是多少m。 
如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,
(1)求证:ΔABF ∽ΔACE
(2)求证:ΔAEF ∽ΔACB
(3)若∠A=60, 求:
小明想利用太阳光测量楼高。他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
已知反比例函数 和一次函数y=-x+a-1(a为常数)
和一次函数y=-x+a-1(a为常数)
(1)当a=5时,求反比例函数与一次函数的交点坐标
(2)是否存在实数a,使反比例函数与一次函数有且只有一个交点,如果存在,求出实数a,如果不存在,说明理由
 ,则
,则 的值为( )
的值为( )


 的方程
的方程 的一个根是
的一个根是 ,则k=
,则k=  是
是 的中位线,
的中位线, 是
是 = .
= .

 粤公网安备 44130202000953号
粤公网安备 44130202000953号