江苏省扬州市江都区八年级下学期期末考试数学试卷
以下问题,不适合用普查的是( )
| A.了解全班同学每周体育锻炼的时间 |
| B.旅客上飞机前的安检 |
| C.学校招聘教师,对应聘人员面试 |
| D.了解全市中小学生每天的零花钱 |
袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球.下列事件是必然事件的是( )
| A.摸出的三个球中至少有一个球是黑球 |
| B.摸出的三个球中至少有一个球是白球 |
| C.摸出的三个球中至少有两个球是黑球 |
| D.摸出的三个球中至少有两个球是白球 |
已知下列命题,其中真命题的个数是( )
①若 ,则
,则 ;
;
②对角线互相垂直平分的四边形是菱形;
③两组对角分别相等的四边形是平行四边形;
④在反比例函数 中,如果函数值y
中,如果函数值y 1时,那么自变量x
1时,那么自变量x 2.
2.
| A.4个 | B.3个 | C.2个 | D.1个 |
教室的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃后停止加热。水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系。直到水温降至20℃,饮水机关机。饮水机关机后即刻自动开机。重复上述自动程序,若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,为了在上午第一节课下课时(8:45)能喝到不超过40℃的水,则接通电源的时间可以是当天上午的( )
| A.7:10 | B.7:20 | C.7:30 | D.7:50 |
如图所示,将一张边长为8的正方形纸片 折叠,使点
折叠,使点 落在
落在 的中点
的中点 处,点
处,点 落在点
落在点 处,折痕为
处,折痕为 ,则线段
,则线段 的长为( )
的长为( )
| A.10 | B.4 |
C. |
D. |
某校为了解该校1000名毕业生的数学考试成绩,从中抽查了100名考生的数学成绩.在这次调查中,样本容量是 .
在下列图形:①圆 ②等边三角形 ③矩形 ④平行四边形中,既是中心对称图形又是轴对称图形的是 (填写序号).
要用反证法证明命题“一个三角形中不可能有两个角是直角”,首先应假设这个三角形中 .
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=3,则DF的长为 .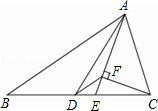
如图,平行四边形 中,点
中,点 在
在 上,以
上,以 为折痕,把△
为折痕,把△ 向上翻折,点
向上翻折,点 正好落在
正好落在 边的点
边的点 处 ,若△
处 ,若△ 的周长为6,△
的周长为6,△ 的周长为20,那么
的周长为20,那么 的长为 .
的长为 .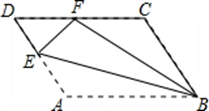
如图,四边形 是矩形,四边形
是矩形,四边形 是正方形,点
是正方形,点 在
在 轴的负半轴上,点
轴的负半轴上,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在
在 上,点
上,点 在反比例函数
在反比例函数 的图像上,正方形
的图像上,正方形 的面积为4,且
的面积为4,且 ,则
,则 值为__ __.
值为__ __.
如图,在方格纸中,△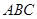 的三个顶点及
的三个顶点及 、五个点分别位于小正方形的顶点上.
、五个点分别位于小正方形的顶点上.
(1)画出△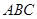 绕点
绕点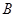 顺时针方向旋转90°后的图形.
顺时针方向旋转90°后的图形.
(2)先从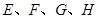 四个点中任意取两个不同的点,再和
四个点中任意取两个不同的点,再和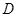 点构成三角形,求所得三角形与△
点构成三角形,求所得三角形与△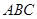 面积相等的概率是 .
面积相等的概率是 .
江都区为了解2014年初中毕业生毕业后的去向,对部分初三学生进行了抽样调查,就初三学生的四种去向(A读普通高中;B读职业高中;C直接进入社会就业;D其它)进行数据统计,并绘制了两幅不完整的统计图(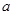 )、(
)、(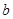 ).请问:
).请问:
(1)该区共调查了 名初中毕业生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该区2014年初三毕业生共有8500人,请估计该区今年的初三毕业生中读普通高中的学生人数.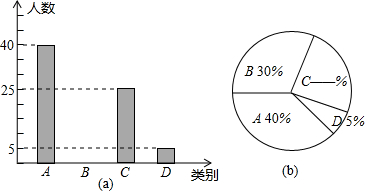
如图所示,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.
(1)求证:OE=CB;
(2)如果OC: OB=1:2,OE=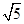 ,求菱形ABCD的面积.
,求菱形ABCD的面积.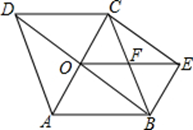
阅读下列材料,然后回答问题:
在进行二次根式运算时,我们有时会碰上如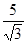 、
、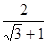 这样的式子,其实我们还可以将其进一步化简:
这样的式子,其实我们还可以将其进一步化简: ;
;  。以上这种化简过程叫做分母有理化。
。以上这种化简过程叫做分母有理化。  还可以用以下方法化简:
还可以用以下方法化简:
(1)请用其中一种方法化简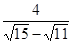
(2)化简: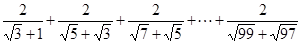
某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)列出原计划种植亩数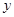 (亩)与平均每亩产量
(亩)与平均每亩产量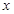 (万斤)之间的函数关系式,并写出自变量
(万斤)之间的函数关系式,并写出自变量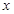 的取值范围;(总产量=亩数
的取值范围;(总产量=亩数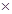 平均每亩产量)
平均每亩产量)
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了8万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
如图,已知直线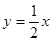 与双曲线
与双曲线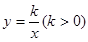 交于
交于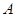 、
、 两点,
两点,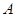 点横坐标为4.
点横坐标为4.
(1)求 值;
值;
(2)直接写出关于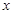 的不等式
的不等式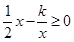 的解集;
的解集;
(3)若双曲线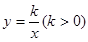 上有一点
上有一点 的纵坐标为8,求△
的纵坐标为8,求△ 的面积.
的面积.
(4)若在 轴上有点
轴上有点 ,
,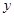 轴上有点
轴上有点 ,且点
,且点 、
、 、
、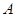 、
、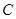 四点恰好构成平行四边形,直接写出点
四点恰好构成平行四边形,直接写出点 、
、 的坐标.
的坐标.


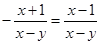

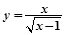 的自变量x的取值范围在数轴上表示为( )
的自变量x的取值范围在数轴上表示为( )
 与反比例函数
与反比例函数 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( ) 
 的最简公分母是_ .
的最简公分母是_ . 在数轴上的位置如图所示,化简
在数轴上的位置如图所示,化简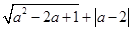 = .
= .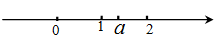
 (
(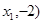 、
、 (
(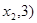 、
、 (
(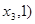 在双曲线
在双曲线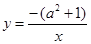 上,那么
上,那么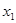 、
、 、
、 的大小关系是_ .
的大小关系是_ . 的方程
的方程 的解为正数,那么
的解为正数,那么 的取值范围是_ .
的取值范围是_ . (2)
(2)

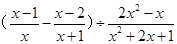 ,其中
,其中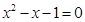
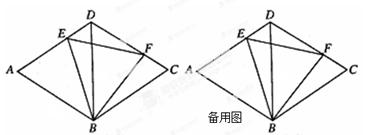
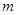 ,则
,则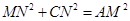
 粤公网安备 44130202000953号
粤公网安备 44130202000953号