浙江省金华十校高二下学期期末考试理科数学试卷
若集合A={x|﹣2<x<1},B={x|0<x<2},则集合A∩B=( )
| A.{x|﹣1<x<1} | B.{x|﹣2<x<1} |
| C.{x|﹣2<x<2} | D.{x|0<x<1} |
在等差数列{an}中,a2=1,a4=5,则{an}的前5项和S5=( )
| A.7 | B.15 | C.20 | D.25 |
函数f(x)=2sinxcosx是( )
| A.最小正周期为2π的奇函数 | B.最小正周期为2π的偶函数 |
| C.最小正周期为π的奇函数 | D.最小正周期为π的偶函数 |
已知向量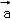 ,
,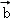 不共线,
不共线,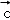 =k
=k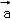 +
+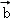 ,(k∈R),
,(k∈R),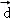 =
=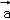 ﹣
﹣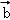 如果
如果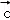 ∥
∥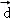 那么( )
那么( )
A.k=﹣1且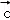 与 与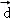 反向 反向 |
B.k=1且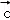 与 与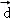 反向 反向 |
C.k=﹣1且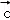 与 与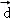 同向 同向 |
D.k=1且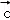 与 与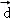 同向 同向 |
已知两条不同的直线m、n,两个不同的平面a、β,则下列命题中的真命题是( )
| A.若m⊥a,n⊥β,a⊥β,则m⊥n |
| B.若m⊥a,n∥β,a⊥β,则m⊥n |
| C.若m∥a,n∥β,a∥β,则m∥n |
| D.若m∥a,n⊥β,a⊥β,则m∥n |
设双曲线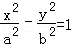 的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
A.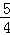 |
B.5 | C.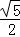 |
D.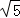 |
若函数y=loga(x2﹣ax+1)有最小值,则a的取值范围是( )
| A.0<a<1 | B.0<a<2,a≠1 | C.1<a<2 | D.a≥2 |
点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中点,且∠EPA=∠D1PD,则点P的轨迹是( )
| A.直线 | B.圆 | C.抛物线 | D.双曲线 |
已知△ABC的顶点A(3,0),B(0,1),C(1,1),P(x,y)在△ABC内部(包括边界),若目标函数z= (a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )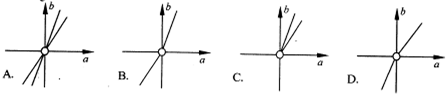
已知点A(﹣2,4),B(4,2),直线l:ax﹣y+8﹣a=0,若直线l与直线AB平行,则a= _________ .
设公比为q(q>0)的等比数列{an}的前n项和为Sn.若S2=3a2+2,S4=3a4+2,则q= _________ .
设某几何体的三视图如图(尺寸的长度单位为m)则该几何体的体积为 _________ m3.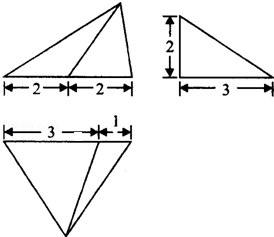
已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l:y=x﹣1被该圆所截得的弦长为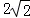 ,则圆C的标准方程为 _________ .
,则圆C的标准方程为 _________ .
已知函数f(x)=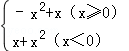 ,对任意的x∈[0,1]恒有f(x+a)≤f(x)成立,则实数a的取值范围是 .
,对任意的x∈[0,1]恒有f(x+a)≤f(x)成立,则实数a的取值范围是 .
在等差数列{an}和等比数列{bn}中,a1=1,b1=2,bn>0(n∈N*),且b1,a2,b2成等差数列,a2,b2,a3+2成等比数列,数列{bn}的前n项和为Sn.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若Sn+an>m对任意的正整数n恒成立,求常数m的取值范围.
已知a,b,c分别为△ABC三个内角A,B,C的对边,acosC+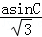 ﹣b=0.
﹣b=0.
(Ⅰ)求A;
(Ⅱ)若△ABC的面积为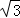 ,求bsinB+csinC的最小值.
,求bsinB+csinC的最小值.
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
(Ⅰ)求证:AB⊥CQ;
(Ⅱ)求BP的长;
(Ⅲ)求直线AP与平面ABC所成的角.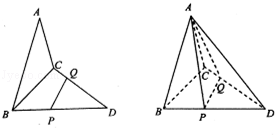
已知椭圆C: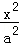 +
+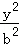 =1(a>b>0),直线l:y=kx+m(k≠0,m≠0),直线l交椭圆C与P,Q两点.
=1(a>b>0),直线l:y=kx+m(k≠0,m≠0),直线l交椭圆C与P,Q两点.
(Ⅰ)若k=1,椭圆C经过点(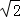 ,1),直线l经过椭圆C的焦点和顶点,求椭圆方程;
,1),直线l经过椭圆C的焦点和顶点,求椭圆方程;
(Ⅱ)若k= ,b=1,且kOP,k,kOQ成等比数列,求三角形OPQ面积S的取值范围.
,b=1,且kOP,k,kOQ成等比数列,求三角形OPQ面积S的取值范围.
 >
>
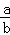 >1
>1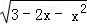 的值域是 _________ .
的值域是 _________ .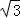 sinxcosx的最大值为 _________ .
sinxcosx的最大值为 _________ . 粤公网安备 44130202000953号
粤公网安备 44130202000953号