高考数学(理)一轮配套特训:3-7正弦定理和余弦定理
在△ABC中,已知sinA∶sinB∶sinC=4∶5∶8,则△ABC一定为( )
| A.正三角形 | B.等腰三角形 |
| C.直角三角形 | D.钝角三角形 |
已知在锐角△ABC中,角A,B,C所对的边分别为a,b,c,且tanC= ,则角C为( )
,则角C为( )
A. |
B. |
C. |
D. |
已知△ABC中,AB= ,BC=1,sinC=
,BC=1,sinC= cosC,则△ABC的面积为( )
cosC,则△ABC的面积为( )
A. |
B. |
C. |
D. |
△ABC的内角A,B,C的对边分别为a,b,c,已知cos(A-C)+cosB=1,a=2c,则C=( )
A. 或
或 B.
B. C.
C. 或
或 D.
D.
在△ABC中,角A,B,C的对边分别为a,b,c.已知a2-c2=2b,且sinB=4cosAsinC,则b的值为( )
| A.4 | B.8 | C.6 | D.10 |
在△ABC中,a,b,c分别是角A,B,C的对边,a,b,c满足b2=a2+c2-ac,若AC=2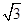 ,则△ABC面积的最大值为( )
,则△ABC面积的最大值为( )
A.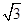 |
B.2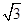 |
C.3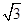 |
D.4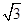 |
在△ABC中,设角A、B、C的对边分别为a、b、c,若a=(cosC,2a-c),b=(b,-cosB)且a⊥b,则B=________.
在△ABC中,内角A、B、C所对的边分别是a、b、c,若sinC+sin(B-A)=sin2A,则△ABC的形状为________.
在△ABC中,a,b,c分别是角A,B,C的对边,已知cos2A-3cos(B+C)=1,若△ABC的面积S=5 ,b=5,则c的值为________.
,b=5,则c的值为________.
在△ABC中,a,b,c分别是三内角A,B,C所对的三边,已知b2+c2=a2+bc.
(1)求角A的大小;
(2)若2sin2 +2sin2
+2sin2 =1,试判断△ABC的形状.
=1,试判断△ABC的形状.
在△ABC中,内角A,B,C的对边分别为a,b,c.已知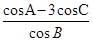 =
=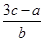 .
.
(1)求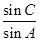 的值;
的值;
(2)若B为钝角,b=10,求a的取值范围.
在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ,sinB=
,sinB= cosC.
cosC.
(1)求tanC的值;
(2)若a= ,求△ABC的面积.
,求△ABC的面积.
已知△ABC的三边长为a,b,c,且面积S△ABC= (b2+c2-a2),则A=( )
(b2+c2-a2),则A=( )
A. |
B. |
C. |
D. |
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC,则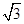 sinA-cos(B+
sinA-cos(B+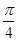 )的最大值为( )
)的最大值为( )
A.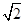 |
B.2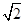 |
C.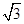 |
D.2 |
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB= BD,BC=2BD,则sinC的值为________.
BD,BC=2BD,则sinC的值为________.
 .
. ,求sinA的值;
,求sinA的值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号