2011-2012年新人教版高一上学期数学
用描述法表示一元二次方程的全体,应是( )
| A.{x|ax2+bx+c=0,a,b,c∈R} |
| B.{x|ax2+bx+c=0,a,b,c∈R,且a≠0} |
| C.{ax2+bx+c=0|a,b,c∈R} |
| D.{ax2+bx+c=0|a,b,c∈R,且a≠0} |
来源:20112012年新人教版高一上学期数学
图中阴影部分所表示的集合是( )
A.B∩[CU(A∪C)] B.(A∪B) ∪(B∪C)
C.(A∪C)∩(CUB) D.[CU(A∩C)]∪B
来源:20112012年新人教版高一上学期数学
设函数f (x)是(- ,+
,+ )上的减函数,又若a
)上的减函数,又若a R,则( )
R,则( )
| A.f (a)>f (2a) | B.f (a2)<f (a) |
| C.f (a2+a)<f (a) | D.f (a2+1)<f (a) |
来源:20112012年新人教版高一上学期数学
(本小题满分12分)
已知,全集U={x|-5≤x≤3},A={x|-5≤x<-1},B={x|-1≤x<1},求CUA,CUB,(CUA)∩(CUB),(CUA)∪(CUB),CU(A∩B),CU(A∪B),并指出其中相关的集合
来源:20112012年新人教版高一上学期数学
(本小题满分12分)
如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x,求此框架围成的面积y与x的函数式y=f (x),并写出它的定义域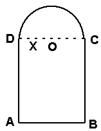
来源:20112012年新人教版高一上学期数学
(本小题满分12分)
已知f(x)是R上的偶函数,且在(0,+  )上单调递增,并且f (x)<0对
)上单调递增,并且f (x)<0对 一切
一切 成立,试判断
成立,试判断 在(-
在(- ,0)上的单调性,并证明你的结论
,0)上的单调性,并证明你的结论
来源:20112012年新人教版高一上学期数学
已知A、B两地相距150千米,某人开汽车以60千米/小时的速度从A地到达B地,在B地停留1小时后再以50千米/小时的速度返回A地,把汽车离开A地的距离x表示为时间t(小时)的函数表达式是( )
A.x=60t B.x=60t+50t
C.x= D.x=
D.x=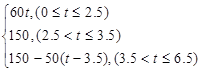
来源:20112012年新人教版高一上学期数学
设函数 的定义域为M,值域为N,那么( )
的定义域为M,值域为N,那么( )
| A.M={x|x≠0},N={y|y≠0} |
B.M={x|x<0且x≠-1,或x>0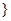 ,N= ,N= y|y<0,或0<y<1,或y>1 y|y<0,或0<y<1,或y>1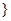 |
| C.M={x|x≠0},N={y|y∈R} |
| D.M={x|x<-1,或-1<x<0,或x>0=,N={y|y≠0} |
来源:20112012年新人教版高一上学期数学
 ,则f(
,则f(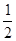 )等于( )
)等于( ) 是( )
是( ) ,若
,若 ,
,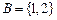 ,则
,则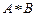 中的所有元素数字之和为 ( )
中的所有元素数字之和为 ( )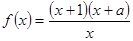 为奇函数,则实数
为奇函数,则实数 ( )
( )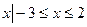 },B={x
},B={x },且A
},且A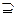 B,则实数k的取值范围是
B,则实数k的取值范围是  2+(K-1)x+3是偶函数,则f(x)的递减区间是
2+(K-1)x+3是偶函数,则f(x)的递减区间是  [0,1],则函数y=
[0,1],则函数y=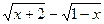 的值域是
的值域是 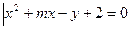 },集合B={(x,y)
},集合B={(x,y) ,且0
,且0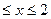 },又A
},又A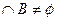 ,求实数m的取值范围
,求实数m的取值范围
 ,求f[f(0)]的值
,求f[f(0)]的值 在
在 上的单调性,并证明之.
上的单调性,并证明之.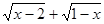 有意义;\
有意义;\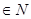 )的图象是一直线;
)的图象是一直线;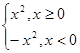 的图象是抛物线,其中正确的命题个数是( )
的图象是抛物线,其中正确的命题个数是( ) 粤公网安备 44130202000953号
粤公网安备 44130202000953号