山东省东营市高三4月统一质量检测考试文科数学试卷
命题“若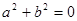 ,
,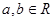 ,则
,则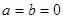 ”的逆否命题是 ( )
”的逆否命题是 ( )
A.若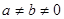 , ,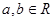 ,则 ,则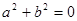 |
B.若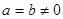 , ,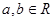 ,则 ,则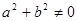 |
C.若 且 且 , ,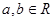 ,则 ,则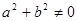 |
D.若 或 或 , ,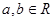 ,则 ,则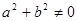 |
来源:2014届山东省东营市高三4月统一质量检测考试文科数学试卷
某种饮料每箱装5听,其中有3听合格,2听不合格,现质检人员从中随机抽取2听进行检测,则检测出至少有一听不合格饮料的概率是( )
A. |
B. |
C. |
D. |
来源:2014届山东省东营市高三4月统一质量检测考试文科数学试卷
已知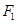 ,
,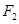 是双曲线
是双曲线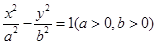 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点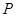 与点
与点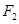 关于直线
关于直线 对称,则该双曲线的离心率为( )
对称,则该双曲线的离心率为( )
A. |
B. |
C.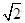 |
D.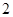 |
来源:2014届山东省东营市高三4月统一质量检测考试文科数学试卷
某公司一年购买某种货物400吨,每次都购买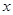 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则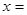 ___ ____ 吨.
___ ____ 吨.
来源:2014届山东省东营市高三4月统一质量检测考试文科数学试卷
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如下表l,表2.
表1:男生“智力评分”频数分布表
| 智力评分 |
 |
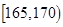 |
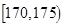 |
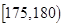 |
 |
 |
| 频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:女生“智力评分”频数分布表
| 智力评分 |
 |
 |
 |
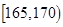 |
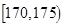 |
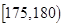 |
| 频数 |
1 |
7 |
12 |
6 |
3 |
1 |
(1)求高一的男生人数并完成下面男生的频率分布直方图;
(2)估计该校学生“智力评分”在[1 65,1 80)之间的概率;
(3)从样本中“智力评分”在[180,190)的男生中任选2人,求至少有1人“智力评分”在[185,190)之间的概率.
来源:2014届山东省东营市高三4月统一质量检测考试文科数学试卷
如图甲,在平面四边形ABCD中,已知
 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.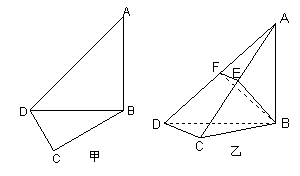
(1)求证:DC 平面ABC;
平面ABC;
(2)设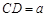 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
来源:2014届山东省东营市高三4月统一质量检测考试文科数学试卷
设数列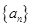 为等差数列,且
为等差数列,且 ,
,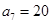 ,数列
,数列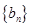 的前
的前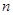 项和为
项和为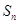 ,
,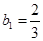 且
且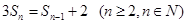
(1)求数列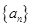 ,
,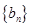 的通项公式;
的通项公式;
(2)若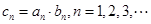 ,求数列
,求数列 的前
的前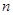 项和
项和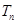 .
.
来源:2014届山东省东营市高三4月统一质量检测考试文科数学试卷
设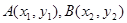 是椭圆
是椭圆 的两点,
的两点,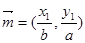 ,
, ,且
,且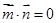 ,椭圆离心率
,椭圆离心率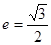 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.
(1)求椭圆方程;
(2)若存在斜率为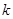 的直线AB过椭圆的焦点
的直线AB过椭圆的焦点 (
( 为半焦距),求
为半焦距),求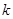 的值;
的值;
(3)试问 的面积是否为定值?若是,求出该定值;若不是,说明理由.
的面积是否为定值?若是,求出该定值;若不是,说明理由.
来源:2014届山东省东营市高三4月统一质量检测考试文科数学试卷
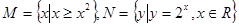 ,则
,则 ( )
( )

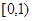

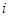 为虚数单位,则
为虚数单位,则 ( )
( )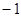
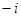
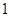
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为 ( )
的最大值为 ( )

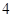

 ,函数
,函数 在
在 上单调递减.则
上单调递减.则 的取值范围是 ( )
的取值范围是 ( )



 ( )
( )




 的部分图像如图所示,则
的部分图像如图所示,则




 满足
满足 ,且在
,且在 时,
时, ,则关于
,则关于 的方程
的方程 在
在 上的根的个数是 ( )
上的根的个数是 ( )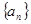 是递增数列,
是递增数列,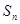 是
是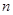 项和.若
项和.若 是方程
是方程 的两个根,则
的两个根,则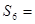 ____ .
____ .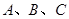 三点在球心为
三点在球心为 的球面上,
的球面上,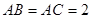 ,
, ,球心
,球心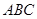 的距离为
的距离为 ,则球
,则球
 分别是
分别是 的斜边
的斜边 上的两个三等分点,已知
上的两个三等分点,已知 ,则
,则 .
. 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足
 的值;
的值;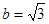 且
且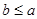 ,求
,求 的取值范围.
的取值范围.
 ,其中
,其中 ,
, 为正整数,
为正整数,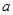 ,
,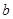 ,
,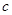 均为常数,曲线
均为常数,曲线 在
在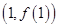 处的切线方程为
处的切线方程为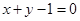 .
.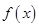 的最大值;
的最大值; 都有
都有 .(
.( 为自然对数的底)
为自然对数的底) 粤公网安备 44130202000953号
粤公网安备 44130202000953号