吉林省长春市高中毕业班第一次调研测试文科试卷
已知集合M={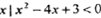 },集合N="{" x|lg(3-x)>0},则
},集合N="{" x|lg(3-x)>0},则 =( )
=( )
| A.{ x|2<x<3} | B.{ x|1<x<3} | C.. { x|1<x<2} | D.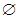 |
某几何体的三视图如右图,(其中侧视图中的圆弧是半圆),则该几何体的表面积为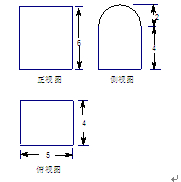
| A.92+14π | B.82+14π |
| C.92+24π | D.82+24π |
等比数列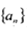 中,
中, 前三项和为S3=27,则公比q的值是( )
前三项和为S3=27,则公比q的值是( )
| A.1 | B.-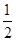 |
C.1或-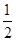 |
D.-1或-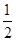 |
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况,设 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求 的分布列和期望.
的分布列和期望.
实数x,y满足 ,若函数z=x+y的最大值为4,则实数a的值为( )
,若函数z=x+y的最大值为4,则实数a的值为( )
| A.2 | B.3 | C. |
D.4 |
已知三条不重合的直线m,n,l 和两个不重合的平面α,β ,下列命题正确的是:( )
A.若m//n,n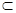 α,则m// α α,则m// α |
B.若α⊥β, α β="m," n⊥m ,则n⊥α. β="m," n⊥m ,则n⊥α. |
| C.若l⊥n ,m⊥n,则l//m |
| D.若l⊥α,m⊥β, 且l⊥m ,则α⊥β |
已知双曲线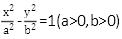 的右顶点、左焦点分别为A、F,点B(0,-b),
的右顶点、左焦点分别为A、F,点B(0,-b),
若 ,则双曲线的离心率值为( )
,则双曲线的离心率值为( )
(A) (B)
(B)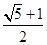 (C)
(C) (D)
(D)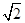
若函数y=f(x)图象上的任意一点p的坐标(x,y)满足条件|x|≥|y|,则称函数具有性质S,那么下列函数中具有性质S的是( )
A.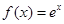 -1 -1 |
B.f(x)=lnx |
| C.f(x)=sinx | D.f(x)=tanx |
已知 设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b
设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b ) 内,,则x2+y2=b-a的面积的最小值为( )
) 内,,则x2+y2=b-a的面积的最小值为( )
A.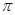 |
B.2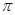 |
C.3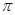 |
D.4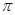 |
已知三棱柱ABC-A1B1C1 底面是边长为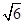 的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12
的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12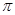 ,则该三棱柱的体积为
,则该三棱柱的体积为
定义[x]表示不超过x的最大整数,例如:[1.5]=1,[-1.5]=-2,若f(x)=sin(x-[x]),则下列结论中①y=f(x)是奇是函数②.y=f(x)是周期函数,周期为2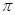 ③..y=f(x)的最小值为0,无最大值④.y=f(x)无最小值,最大值为sin1.正确的序号为.
③..y=f(x)的最小值为0,无最大值④.y=f(x)无最小值,最大值为sin1.正确的序号为.
已知向量 ,设函数
,设函数 .
.
(1).求函数f(x)的最小正周期;
(2).已知a,b,c分别为三角形ABC的内角对应的三边长,A为锐角,a=1, ,且
,且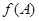 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积.
如图,E是以AB为直径的半圆弧上异于A,B的点,矩形ABCD所在平面垂直于该半圆所在的平面,且AB=2AD=2。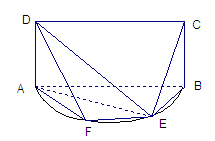
(1).求证:EA⊥EC;
(2).设平面ECD与半圆弧的另一个交点为F。
①求证:EF//AB;
②若EF=1,求三棱锥E—ADF的体积
已知平面上的动点P(x,y)及两个定点A(-2,0),B(2,0),直线PA,PB的斜率分别为K1,K2且K1K2=-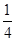
(1).求动点P的轨迹C方程;
(2).设直线L:y=kx+m与曲线C交于不同两点,M,N,当OM⊥ON时,求O点到直线L的距离(O为坐标原点)
已知函数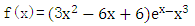
(1).求函数f(x)的单调区间及极值;
(2).若x1≠x2满足f(x1)=f(x2),求证:x1+x2<0
如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于F,连接CF并延长交AB于点E.
(1).求证:E为AB的中点;
(2).求线段FB的长.
以直角坐标系的原点为极点O,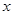 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为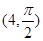 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.

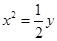 的焦点到准线的距离是( )
的焦点到准线的距离是( )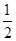
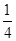
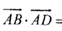 =___
=___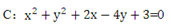 ,关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值为
,关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值为 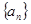 是等差数列,且
是等差数列,且 且
且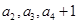 成等比数列。
成等比数列。 ,求前n项和
,求前n项和 .
. M时,证明:2|a+b|<|4+ab|.
M时,证明:2|a+b|<|4+ab|. 粤公网安备 44130202000953号
粤公网安备 44130202000953号