北京市顺义区高三第一次统练文科数学试卷
某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )
| A.8万元 | B.10万元 | C.12万元 | D.15万 |
来源:2014届北京市顺义区高三第一次统练文科数学试卷
已知向量 ,
,  ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2014届北京市顺义区高三第一次统练文科数学试卷
设数集 同时满足条件
同时满足条件
① 中不含元素
中不含元素 ,②若
,②若 ,则
,则 .
.
则下列结论正确的是 ( )
A.集合 中至多有2个元素; 中至多有2个元素; |
B.集合 中至多有3个元素; 中至多有3个元素; |
C.集合 中有且仅有4个元素; 中有且仅有4个元素; |
D.集合 中有无穷多个元素. 中有无穷多个元素. |
来源:2014届北京市顺义区高三第一次统练文科数学试卷
设等比数列 满足公比
满足公比 ,
, ,且数列
,且数列 中任意两项之积也是该数列的一项.若
中任意两项之积也是该数列的一项.若 ,则
,则 的所有可能取值之和为_______________.
的所有可能取值之和为_______________.
来源:2014届北京市顺义区高三第一次统练文科数学试卷
已知关于 的一次函数
的一次函数
(1)设集合 和
和 ,分别从集合
,分别从集合 和
和 中随机取一个数作为
中随机取一个数作为 ,
, ,求函数
,求函数 是增函数的概率;
是增函数的概率;
(2)若实数 ,
, 满足条件
满足条件 ,求函数
,求函数 的图象不经过第四象限的概率.
的图象不经过第四象限的概率.
来源:2014届北京市顺义区高三第一次统练文科数学试卷
如图在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
,
 ,点
,点 是
是 中点,点
中点,点 是
是 边上的任意一点.
边上的任意一点.
(1)当点 为
为 边的中点时,判断
边的中点时,判断 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)证明:无论点 在
在 边的何处,都有
边的何处,都有 ;
;
(3)求三棱锥 的体积.
的体积.
来源:2014届北京市顺义区高三第一次统练文科数学试卷
已知函数 ,(其中常数
,(其中常数 )
)
(1)当 时,求曲线在
时,求曲线在 处的切线方程;
处的切线方程;
(2)若存在实数 使得不等式
使得不等式 成立,求
成立,求 的取值范围.
的取值范围.
来源:2014届北京市顺义区高三第一次统练文科数学试卷
已知椭圆 的离心率
的离心率 ,长轴的左右端点分别为
,长轴的左右端点分别为 ,
, .
.
(1)求椭圆 的方程;
的方程;
(2)设动直线 与曲线
与曲线 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 .
.
求证:以 为直径的圆过定点
为直径的圆过定点 .
.
来源:2014届北京市顺义区高三第一次统练文科数学试卷
 ,
, ,则集合
,则集合 ( )
( )



 为虚数单位,在复平面内复数
为虚数单位,在复平面内复数 对应点的坐标为
对应点的坐标为 
















 的焦点垂直于
的焦点垂直于 轴的弦长为
轴的弦长为 ,则双曲线
,则双曲线 的离心率
的离心率 的值是( )
的值是( )



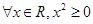 ”的否定是_________________.
”的否定是_________________. 上一点
上一点 的横坐标为
的横坐标为 ,则点
,则点

 (
( )的最小正周期为_____,最大值为____.
)的最小正周期为_____,最大值为____. 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最小值为___________.
的最小值为___________. 中,角
中,角 ,
, ,
, 所对的边分别为为
所对的边分别为为 ,
, ,
, ,且
,且
 ,
, ,求
,求 个实数组成的
个实数组成的 行
行
 ,
, ,
,

 ,再将首项为
,再将首项为 公比为
公比为 的数列
的数列 依次填入第一列的空格内,然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规律填写其它空格
依次填入第一列的空格内,然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规律填写其它空格



 .试用
.试用 表示
表示 的值;
的值; ,记为数列
,记为数列 .
. ;
; 项
项 (
( )成等比数列?若能找到,
)成等比数列?若能找到, 粤公网安备 44130202000953号
粤公网安备 44130202000953号