高考数学文复习二轮作业手册新课标·通用版限时集7讲练习卷

已知sin10°＝k，则sin 70°＝(　　)

已知sin α＝－，且α是第三象限角，则sin 2α－tan α＝(　　)

A．

B．

C．

D．

设sin＝，则sin 2θ＝(　　)

A．－

B．－

C．

D．

函数f(x)＝sin x－cos的值域为(　　)

A．[－2，2]

B．[－，]

C．[－1，1]

D．

将函数y＝sin的图像上各点向右平移个单位，则得到新函数的解析式为(　　)

A．y＝sin

B．y＝sin

C．y＝sin

D．y＝sin

为得到函数y＝cos的图像，只需要将函数y＝sin 2x的图像(　　)

A．向左平移个单位	B．向右平移个单位
C．向左平移个单位	D．向右平移个单位

要得到函数y＝cos(2x＋1)的图像，只要将函数y＝cos 2x的图像(　　)

A．向左平移1个单位	B．向右平移1个单位
C．向左平移个单位	D．向右平移个单位

已知ω>0，0<φ<π，直线x＝和x＝是函数f(x)＝sin(ωx＋φ)图像的两条相邻的对称轴，则φ＝(　　)

A．

B．

C．

D．

关于函数f(x)＝sin与函数g(x)＝cos，下列说法正确的是(　　)

A．函数f(x)和g(x)的图像有一个交点在y轴上

B．函数f(x)和g(x)的图像在区间(0，π)内有3个交点

C．函数f(x)和g(x)的图像关于直线x＝对称

D．函数f(x)和g(x)的图像关于原点(0，0)对称

若函数f(x)＝sin ωx＋cos ωx(x∈R，ω>0)满足f(α)＝－2，f(β)＝0，且|α－β|的最小值为，则函数f(x)的单调递增区间为________．

如图所示的是函数f(x)＝2sin(ωx＋φ)(ω>0，0≤φ≤)的部分图像，其中A，B两点之间的距离为5，那么f(－1)＝________．

图表示的是函数y＝Asin(ωx＋φ)(ω>0，－π<φ<π)的图像的一段，O是坐标原点，P是图像的最高点，M点的坐标为(5，0)，若||＝，·＝15，则此函数的解析式为________．

已知函数f(x)＝.
(1)求函数f(x)的定义域；
(2)设α是第四象限的角，且tan α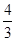＝－，求f(α)的值．

已知函数f(x)＝sin(ωx＋φ)(ω>0，|φ|<π)的部分图像如图所示，

(1)求ω，φ的值；
(2)设g(x)＝2f f－1，当x∈[0，]时，求函数g(x)的值域．

已知函数f(x)＝cos＋2sin²x，x∈R.
(1)求函数f(x)的最小正周期及对称轴方程；
(2)当x∈时，求函数f(x)的最大值和最小值及相应的x值．