[北京]2014届北京市东城区高三上学期期末统一检测理科数学试卷
设 ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行”的( )
平行”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
来源:2014届北京市东城区高三上学期期末统一检测理科数学试卷
设等差数列 满足:公差
满足:公差 ,
, ,且
,且 中任意两项之和也是该数列中的一项.若
中任意两项之和也是该数列中的一项.若 ,则
,则 ; 若
; 若 ,则
,则 的所有可能取值之和为 .
的所有可能取值之和为 .
来源:2014届北京市东城区高三上学期期末统一检测理科数学试卷
已知 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足 ,
,  .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足:
满足:
 ,求数列
,求数列 的前
的前 项和.
项和.
来源:2014届北京市东城区高三上学期期末统一检测理科数学试卷
如图,在三棱柱 中,
中, 平面
平面 ,
, ,
, ,
,  ,
, 分别是
分别是 ,
, 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
来源:2014届北京市东城区高三上学期期末统一检测理科数学试卷
已知椭圆
 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点 ,
, ,若
,若 ,求△
,求△ 的面积.
的面积.
来源:2014届北京市东城区高三上学期期末统一检测理科数学试卷
 ,
, ,则
,则 ( )
( )



 的对应点位于( )
的对应点位于( )




 中,
中, ,
, ,
, ,则
,则 ( )
( )



 与圆
与圆 相交于
相交于 ,
, 两点,若
两点,若 ,则
,则 的取值范围为( )
的取值范围为( )



 中,
中, ,
, ,
, ,
, ,点
,点 在线段
在线段 上,若
上,若 ,则
,则 的取值范围是( )
的取值范围是( )



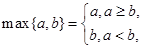 设实数
设实数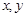 满足约束条件
满足约束条件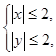 则
则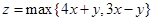 的取值范围是( )
的取值范围是( )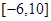
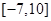
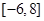
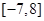
 为奇函数,当
为奇函数,当 时,
时, ,则
,则 的值为 .
的值为 .
 为抛物线
为抛物线 上一点,则抛物线焦点坐标为 ;点
上一点,则抛物线焦点坐标为 ;点 到抛物线的准线的距离为 .
到抛物线的准线的距离为 . 的最大值为 .
的最大值为 . ,点
,点 在曲线
在曲线 上,若阴影部分面积与△
上,若阴影部分面积与△ 面积相等时,则
面积相等时,则 .
. 
 .
. 的值;
的值; 在区间
在区间 上的最大值和最小值.
上的最大值和最小值. ,函数
,函数 .
. 时,求
时,求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围. 满足:①对任意
满足:①对任意 ,
, ;②存在常数
;②存在常数 ,对任意
,对任意 ,则称数列
,则称数列 数列”.
数列”.
 ,证明:数列
,证明:数列 ;
; ,数列
,数列 为等差数列.
为等差数列. 粤公网安备 44130202000953号
粤公网安备 44130202000953号