[湖南]2013-2014学年湖南张家界普通高中高一上学期期末联考数学卷
根据表格中的数据,可以断定方程 的一个根所在的区间是( )
的一个根所在的区间是( )
 |
-1 |
0 |
1 |
2 |
3 |
 |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
 |
1 |
2 |
3 |
4 |
5 |
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
来源:2013-2014学年湖南张家界普通高中高一上学期期末联考数学卷
要得到函数 的图像,只须将函数
的图像,只须将函数 的图像( )
的图像( )
A.向左平移 |
B.向右平移 |
C.向左平移 |
D.向右平移 |
来源:2013-2014学年湖南张家界普通高中高一上学期期末联考数学卷
某校要召开学生代表大会,规定各班每10人推选一名代表,当班人数除以10的余数大于6时,再增选一名代表,则各班推选代表人数 与该班人数
与该班人数 之间的函数关系用取整函数
之间的函数关系用取整函数 (
( 表示不大于
表示不大于 的最大整数,如
的最大整数,如 )可表示为( )
)可表示为( )
A. |
B. |
C. |
D. |
来源:2013-2014学年湖南张家界普通高中高一上学期期末联考数学卷
在平行四边形 中,
中, 与
与 交于点
交于点 ,
, 为线段
为线段 的中点,
的中点, 的延长线交
的延长线交 于
于 .设
.设 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
来源:2013-2014学年湖南张家界普通高中高一上学期期末联考数学卷
设 是整数集的一个非空子集,对于
是整数集的一个非空子集,对于 ,若
,若 ,且
,且 ,则称
,则称 是
是 的一个“孤立元”。给定集合
的一个“孤立元”。给定集合 ,在由
,在由 的三个元素构成的所有集合中,不含“孤立元”的集合个数为 .
的三个元素构成的所有集合中,不含“孤立元”的集合个数为 .
来源:2013-2014学年湖南张家界普通高中高一上学期期末联考数学卷
规定满足“ ”的分段函数
”的分段函数 叫做“对偶函数”,已知函数
叫做“对偶函数”,已知函数 是“对偶函数”,则(1)
是“对偶函数”,则(1) ;
;
(2)若 对任意正整数
对任意正整数 都成立,实数
都成立,实数 的取值范围为 .
的取值范围为 .
来源:2013-2014学年湖南张家界普通高中高一上学期期末联考数学卷
我国是水资源较贫乏的国家之一,各地采用价格调控等手段来达到节约用水的目的,某市每户每月用水收费办法是:水费=基本费+超额费+定额损耗费.且有如下两条规定:
①若每月用水量不超过最低限量 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元;
②若用水量超过 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费.
解答以下问题:(1)写出每月水费 (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2)若该市某家庭今年一季度每月的用水量和支付的费用如下表所示:
| 月份 |
用水量(立方米) |
水费(元) |
| 一 |
5 |
17 |
| 二 |
6 |
22 |
| 三 |
 |
12 |
试判断该家庭今年一、二、三各月份的用水量是否超过最低限量,并求 的值.
的值.
来源:2013-2014学年湖南张家界普通高中高一上学期期末联考数学卷
 ,则
,则 ( )
( )



 的最小正周期为( )
的最小正周期为( )







 的终边过点
的终边过点 ,则
,则 的值为( )
的值为( )



 ,
, ,则
,则 .
. .
. 的定义域为 .
的定义域为 .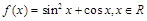 的最大值等于 .
的最大值等于 . 为锐角,且
为锐角,且 ,则
,则 .
. ,若
,若 ,(1)求
,(1)求 的值; (2)求
的值; (2)求 .
.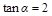 ,求下列各式的值:(1)
,求下列各式的值:(1) ;(2)
;(2)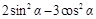 .
.
 为
为 的中点,
的中点, ,求
,求 的值;
的值; 是以
是以 为斜边的直角三角形,求
为斜边的直角三角形,求 的值.
的值. ;
; 求
求 的值.
的值. 满足
满足 且
且 .
. ,并求
,并求 的取值范围;
的取值范围; 在
在 内至少有一个零点;
内至少有一个零点; 是函数
是函数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号