[广东]2013-2014学年广东惠州市高一第一学期期末考试数学试卷
已知三角形 中,
中, ,则三角形
,则三角形 的形状为( ).
的形状为( ).
| A.钝角三角形 | B.直角三角形 | C.锐角三角形 | D.等腰直角三角形 |
来源:2013-2014学年广东惠州市高一第一学期期末考试数学试卷
集合 ,
, ,给出下列四个图形,其中能表示以
,给出下列四个图形,其中能表示以 为定义域,
为定义域, 为值域的函数关系的是( ).
为值域的函数关系的是( ).
A. B. C. D.
来源:2013-2014学年广东惠州市高一第一学期期末考试数学试卷
要由函数 的图象得到函数
的图象得到函数 的图象,下列变换正确的是( )
的图象,下列变换正确的是( )
A.向左平移 个单位长度,再将各点横坐标变为原来的 个单位长度,再将各点横坐标变为原来的 倍. 倍. |
B.向左平移 个单位长度,再将各点横坐标变为原来的 个单位长度,再将各点横坐标变为原来的 . . |
C.向右平移 个单位长度,再将各点横坐标变为原来的 个单位长度,再将各点横坐标变为原来的 倍. 倍. |
D.向右平移 个单位长度,再将各点横坐标变为原来的 个单位长度,再将各点横坐标变为原来的 . . |
来源:2013-2014学年广东惠州市高一第一学期期末考试数学试卷
设 是
是 上的任意函数,下列叙述正确的是( )
上的任意函数,下列叙述正确的是( )
A. 是奇函数 是奇函数 |
B. 是奇函数 是奇函数 |
C. 是偶函数 是偶函数 |
D. 是偶函数 是偶函数 |
来源:2013-2014学年广东惠州市高一第一学期期末考试数学试卷
已知函数 的最大值为2,周期为
的最大值为2,周期为 .
.
(1)确定函数 的解析式,并由此求出函数的单调增区间;
的解析式,并由此求出函数的单调增区间;
(2)若 ,求
,求 的值.
的值.
来源:2013-2014学年广东惠州市高一第一学期期末考试数学试卷
已知函数 .
.
(1)求函数定义域和函数图像所过的定点;
(2)若已知 时,函数最大值为2,求
时,函数最大值为2,求 的值.
的值.
来源:2013-2014学年广东惠州市高一第一学期期末考试数学试卷
某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水, 小时内供水总量为
小时内供水总量为 吨(
吨( ),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
来源:2013-2014学年广东惠州市高一第一学期期末考试数学试卷
设函数 (
( ).
).
(1)若 为偶函数,求实数
为偶函数,求实数 的值;
的值;
(2)已知 ,若对任意
,若对任意 都有
都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
来源:2013-2014学年广东惠州市高一第一学期期末考试数学试卷
 ,
, ,则
,则 ( ).
( ).



 的终边过点
的终边过点 ,
, 的值为( ).
的值为( ).



 ,则
,则 ( )
( )


 的零点所在的区间是( )
的零点所在的区间是( )



 的图象是 ( )
的图象是 ( )




 ,则
,则 __________.
__________. ,且
,且 ,则
,则 __________.
__________. ,则
,则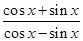 =__________.
=__________. ,
, 若不存在
若不存在 ,使得
,使得 与
与 同时成立,则实数
同时成立,则实数 的取值范围是 .
的取值范围是 . .
. 及
及 ;
; 与
与 的值.
的值. 满足:对任意
满足:对任意 ,都有
,都有 成立,且
成立,且 时,
时, .
. 的值,并证明:当
的值,并证明:当 时,
时, ;
; 在
在 上递减,求实数
上递减,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号