[广东]2014届广东省深圳市宝安区高三上学期调研考试理科数学试卷
为了了解深圳市高三学生的身体发育情况,抽查了该地区100名年龄为17.5—18岁的男生体重(kg),得到频率分布直方图如下:
根据上图可得这100名学生中,体重在[56.5,64.5]的学生人数是( )
A. |
B. |
C. |
D. |
来源:2014届广东省深圳市宝安区高三上学期调研考试理科数学试卷
函数 是( )
是( )
A.最小正周期为 的奇函数 的奇函数 |
B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的偶函数 的偶函数 |
来源:2014届广东省深圳市宝安区高三上学期调研考试理科数学试卷
给出下列关于互不相同的直线 和平面
和平面 的四个命题:
的四个命题:
①若 ,
, ,点
,点 ,则
,则 与
与 不共面;
不共面;
②若 、
、 是异面直线,
是异面直线, ,
, ,且
,且 ,
, ,则
,则 ;
;
③若 ,则
,则 ;
;
④若 ,
, ,
, ,
, ,
, ,则
,则 .
.
其中为假命题的是( )
| A.① | B.② | C.④ | D.③ |
来源:2014届广东省深圳市宝安区高三上学期调研考试理科数学试卷
为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 |
北京 |
上海 |
天津 |
广州 |
| 人数 |
4 |
6 |
3 |
5 |
(1)从这18名对员中随机选出两名,求两人来自同一个队的概率;
(2)比赛结束后,若要求选出两名队员代表发言,设其中来自北京的人数为 ,求随机变量
,求随机变量 的分布列,及数学期望.
的分布列,及数学期望.
来源:2014届广东省深圳市宝安区高三上学期调研考试理科数学试卷
已知点 直线
直线 ,
, 为平面上的动点,过点
为平面上的动点,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,且
,且 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2) 、
、 是轨迹
是轨迹 上异于坐标原点
上异于坐标原点 的不同两点,轨迹
的不同两点,轨迹 在点
在点 、
、 处的切线分别为
处的切线分别为 、
、 ,且
,且 ,
, 、
、 相交于点
相交于点 ,求点
,求点 的纵坐标.
的纵坐标.
来源:2014届广东省深圳市宝安区高三上学期调研考试理科数学试卷
 ,集合
,集合 ,
, ,则
,则 ( )
( )



 其中
其中 是虚数单位)
是虚数单位) ( )
( )



 ,
, ,则向量
,则向量 ( )
( )







 是254,则①应为( ).
是254,则①应为( ).




 的几何体的三视图,则
的几何体的三视图,则
 .
.
 ,
, ,则
,则 的值为__________.
的值为__________. 为等差数列,若
为等差数列,若 ,则
,则 的值为________.
的值为________. 的焦点为圆心,且与双曲线
的焦点为圆心,且与双曲线 的两条渐近线都相切的圆的方程为 .
的两条渐近线都相切的圆的方程为 . 、
、 满足
满足 ,若目标函数
,若目标函数 取得最大值
取得最大值 ,则实数
,则实数 的值为________.
的值为________. 的割线
的割线 交⊙
交⊙ 、
、 两点,割线
两点,割线 经过圆心
经过圆心 ,
, ,
, ,则⊙
,则⊙

 作圆
作圆 的切线,则切线的极坐标方程为________________.
的切线,则切线的极坐标方程为________________. 的部分图像如图所示.
的部分图像如图所示.
 的解析式;
的解析式;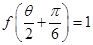 ,
, ,求
,求 .
. 中,
中, 平面
平面 ,
,
 ,
, ,
, 为
为 中点.
中点.
 平面
平面 ;
; 的正弦值.
的正弦值. 的前
的前 项和为
项和为 ,且
,且 .
. 求证:
求证: .
. .
. 在
在 和
和 处的切线相互平行,求
处的切线相互平行,求 的值;
的值; ,对任意的
,对任意的 ,均存在
,均存在 ,使得
,使得 .试求实数
.试求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号