[广东]2014届广东省百所高中高三11月联考理科数学试卷
设 、
、 分别为双曲线
分别为双曲线 的左、右焦点,
的左、右焦点, 为双曲线的左顶点,以
为双曲线的左顶点,以 为直径的圆交双曲线某条渐过线
为直径的圆交双曲线某条渐过线 、
、 两点,且满足
两点,且满足 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A. |
B. |
C. |
D. |
来源:2014届广东省百所高中高三11月联考理科数学试卷
在整数集 中,被
中,被 除所得余数为
除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为 ,则
,则 ,
, 、
、 、
、 、
、 、
、 ,则下列结论错误的是( )
,则下列结论错误的是( )
A. |
B. |
C.“整数 、 、 属于同一‘类’”的充要条件是“ 属于同一‘类’”的充要条件是“ ” ” |
D.命题“整数 、 、 满足 满足 , , ,则 ,则 ”的原命题与逆命题都为真命题 ”的原命题与逆命题都为真命题 |
来源:2014届广东省百所高中高三11月联考理科数学试卷
在极坐标系中,圆 的方程为
的方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为 轴的正半轴建立平面坐标系,圆
轴的正半轴建立平面坐标系,圆 的参数方程
的参数方程 (
( 为参数),若圆
为参数),若圆 与
与 相切,则实数
相切,则实数 .
.
来源:2014届广东省百所高中高三11月联考理科数学试卷
为贯彻“激情工作,快乐生物”的理念,某单位在工作之余举行趣味知识有奖竞赛,比赛分初赛和决赛两部分,为了增加节目的趣味性,初赛采用选手选—题答—题的方式进行,每位选手最多有5次选答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题的正确率为 .
.
(1)求选手甲答题次数不超过4次可进入决赛的概率;
(2)设选手甲在初赛中答题的个数 ,试写出
,试写出 的分布列,并求
的分布列,并求 的数学期望。
的数学期望。
来源:2014届广东省百所高中高三11月联考理科数学试卷
已知数列 的通项公式为
的通项公式为 ,在等差数列数列
,在等差数列数列 中,
中, ,且
,且 ,又
,又 、
、 、
、 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
来源:2014届广东省百所高中高三11月联考理科数学试卷
已知椭圆
 的离心率为
的离心率为 ,直线
,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆
的短半轴长为半径的圆 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)抛物线 与椭圆
与椭圆 有公共焦点,设
有公共焦点,设 与
与 轴交于点
轴交于点 ,不同的两点
,不同的两点 、
、 在
在 上(
上( 、
、 与
与 不重合),且满足
不重合),且满足 ,求
,求 的取值范围.
的取值范围.
来源:2014届广东省百所高中高三11月联考理科数学试卷
 ,
, ,则( )
,则( )



 ,则
,则 在复平面内对应的点位于( )
在复平面内对应的点位于( ) 上为增函数的是 ( )
上为增函数的是 ( )



 中,
中, ,
, ,
, 是
是 的中点,则
的中点,则 等于( )
等于( )






 、
、 满足约束条件
满足约束条件 ,则
,则 的最小值是( )
的最小值是( )



 的值域为 .
的值域为 . 的展开式中常数项是 .
的展开式中常数项是 . 在点
在点 处的切线方程为 .
处的切线方程为 . 的前
的前 项和为
项和为 ,则数列
,则数列 为 .
为 . 指向①时,输出的结果
指向①时,输出的结果 ,当箭头
,当箭头 ,则
,则 .
.
 中,
中, ,
, ,圆
,圆 过
过 、
、 两点且与
两点且与 相切于点
相切于点 交于点
交于点 ,连结
,连结 ,若
,若 ,则
,则 .
.
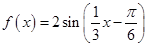 ,
, .
.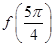 的值;
的值; 、
、 ,
,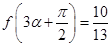 ,
,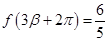 ,求
,求 的值.
的值. 的底面
的底面 是正方形,
是正方形, 平面
平面 为
为 上的点,且
上的点,且 .
.
 ;
; ,求二面角
,求二面角 的余弦值.
的余弦值. ,
, .
. ,求证:当
,求证:当 时,
时, ;
; 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号