[江苏]2014届江苏省江阴市华士片九年级上学期期中考试数学试卷
已知一元二次方程 有两个不相等的实数根,则k的范围是( )
有两个不相等的实数根,则k的范围是( )
A.k> |
B.k< |
C.k≤ 且k≠0 且k≠0 |
D.k< 且k≠0 且k≠0 |
下列命题中正确的是( )
| A.一组对边平行的四边形是平行四边形 |
| B.两条对角线相等的平行四边形是矩形 |
| C.两边相等的平行四边形是菱形 |
| D.对角线互相垂直且相等的四边形是正方形 |
如图, ABCD的周长为
ABCD的周长为 ,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A、4 B、6
B、6 C、8
C、8 D、5
D、5
如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
| A.CM=DM | B. |
C.∠ACD=∠ADC | D.OM=BM |
如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,若EF=3则梯形ABCD的周长为( )
| A.12 | B.10.5 | C.9 | D.15 |
已知⊙O是以原点为圆心, 为半径的圆,点P是直线
为半径的圆,点P是直线 上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
| A.3 | B.4 | C. |
D. |
某种药品连续两次降价后,由每盒200元下调到每盒128元,若每次的降价的百分率相同,设这种药品每次降价的百分率为x,则可列方程为
如图,等腰△ABC的顶角∠A=40°,以AB为直径的半圆与BC、AC分别交于D、E两点,则∠EBC= °
如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM,CN,MN,若AB=2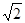 ,BC=2
,BC=2 ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 
已知直线 (n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3++S2012= .
(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3++S2012= .
如图:已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长 .
李丽、陈伟两位同学九年级10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如下图所示:
(1)根据上图中提供的数据填写下表:
| |
平均成绩 |
中位数 |
众数 |
方差(S2) |
| 李丽 |
|
|
80 |
|
| 陈伟 |
|
85 |
|
260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率较高的同学是:
(3)你如何看待这两位同学这一阶段的数学学习,请分别给他们一条合理的建议.
将分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌面上.
(1)随机抽取一张,求抽到偶数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,恰好这个两位数能被3整除的概率是多少?
如图,△ABC中,D是AB边上一点,⊙O过D、B、C三点,ÐDOC=2ÐACD=90°.

(1)求证:直线AC是⊙O的切线;
(2)如果ÐACB=75°,⊙O的半径为2,求BD的长.
某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低x元.
(1)填表:
| 时间 |
第一个月 |
第二个月 |
清仓 |
| 单价(元) |
80 |
|
40 |
| 销售量(件) |
200 |
|
|
(2)如果批发商希望通过销售这批T恤获利9 000元,那么第二个月的单价应是多少元?
国家推行“节能减排,低碳经济”的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元.据市场调查知:每辆车改装前、后的燃料费(含改装费) 、
、 (单位:元)与正常运营时间
(单位:元)与正常运营时间 (单位:天)之间分别满足关系式:
(单位:天)之间分别满足关系式: 、
、 ,如图所示.
,如图所示.
试根据图像解决下列问题:
(1)每辆车改装前每天的燃料费 = 元,每辆车的改装费b= 元.正常运营 天后,就可以从节省燃料费中收回改装成本.
= 元,每辆车的改装费b= 元.正常运营 天后,就可以从节省燃料费中收回改装成本.
(2)某出租汽车公司一次性改装了100辆车,因而,正常运营多少天后共节省燃料费40万元?
如果我们定义:“到三角形的两个顶点距离相等的点,叫做此三角形的开心点。”那么:
(1)如图1,观察并思考,△ABC的开心点有 个
(2)如图2,CD为等边三角形ABC的高,开心点P在高CD上,且PD= ,则∠APB的度数为
,则∠APB的度数为
(3)已知△ABC为直角三角形,斜边BC=5,AB=3,开心点P在AC边上,试探究PA的长。
 有意义的
有意义的 的范围是( )
的范围是( )







 是同类二次根式的是( )
是同类二次根式的是( )



 的解是 ( )
的解是 ( )



 ,则
,则 的值为 .
的值为 . 的两个根,则这个△ABC的周长是
的两个根,则这个△ABC的周长是 
 (2)
(2)
 (配方法) (2)
(配方法) (2) (公式法)
(公式法)
 时,S与t之间的函数关系式.
时,S与t之间的函数关系式. 粤公网安备 44130202000953号
粤公网安备 44130202000953号