[北京]2014届北京市东城区普通校高三上学期期中联考文科数学试卷
若 ,则“
,则“ ”是“
”是“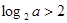 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2014届北京市东城区普通校高三上学期期中联考文科数学试卷
关于函数 ,给出下列四个命题:
,给出下列四个命题:
① ,
, 时,
时, 只有一个实数根;
只有一个实数根;
② 时,
时, 是奇函数;
是奇函数;
③ 的图象关于点
的图象关于点 ,
, 对称;
对称;
④函数 至多有两个零点.
至多有两个零点.
其中正确的命题序号为______________.
来源:2014届北京市东城区普通校高三上学期期中联考文科数学试卷
已知等差数列 的前
的前 项和为
项和为 ,公差
,公差 ,
, ,且
,且 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和公式.
项和公式.
来源:2014届北京市东城区普通校高三上学期期中联考文科数学试卷
已知函数
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的极值;
的极值;
(Ⅲ)对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
来源:2014届北京市东城区普通校高三上学期期中联考文科数学试卷
 ,
, ,则
,则 = ( )
= ( )



 ,则下列不等式正确的是( )
,则下列不等式正确的是( )



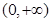 单调递增的函数是( )
单调递增的函数是( )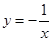


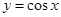
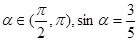 ,则
,则 等于( )
等于( )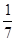
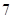


 ,当
,当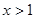 时,
时, 的大小关系为( )
的大小关系为( )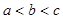

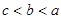
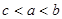
 的边长为
的边长为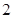 ,
, 为
为 的中点,则
的中点,则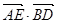 = ( )
= ( )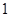
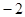

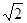
 ,
, 满足
满足 ,且
,且 上的导数满足
上的导数满足 ,则不等式
,则不等式 的解为( )
的解为( )



 在原点处的切线方程是
在原点处的切线方程是 ,则实数
,则实数 .
. ,
, ,b=(-
,b=(- ,
, ),则
),则  a·b
a·b
 b
b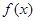 是周期为2的奇函数,当
是周期为2的奇函数,当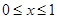 时,
时, ,则
,则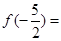 .
. 是公比为
是公比为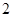 的等比数列,若
的等比数列,若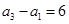 ,则
,则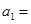 ;
;  ______________.
______________.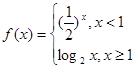 的值域为______________.
的值域为______________. ,
,
 的值;
的值; 的最大值和最小值.
的最大值和最小值. 中,角A、B,C,所对的边分别为
中,角A、B,C,所对的边分别为 ,且
,且
 的值;
的值; ,求
,求 ,函数
,函数 .
. 的值;
的值; 的单调区间.
的单调区间. 是首项为
是首项为 ,公比
,公比 的等比数列.设
的等比数列.设 ,
, ,数列
,数列 满足
满足 ;
; 成等差数列;
成等差数列; 项和
项和 ;
; 对一切正整数
对一切正整数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号