河北省秦皇岛市第二学期期末质量检测试题高二理科数学试卷
正三角形ABC的边长为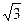 ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
 如图,在边长为
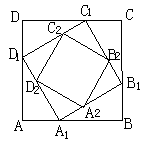
如图,在边长为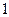 的正方形ABCD中的四条边上有A1、B1、C1、D1四点,分别把AB、BC、CD、DA分成1:2,得到一个小正方形A1B1C1D1,再用同样的方法在正方形A1B1C1D1内做正方形A2B2C2D2,…,这样无限的做下去,则所有这些正方形面积之和为 .
的正方形ABCD中的四条边上有A1、B1、C1、D1四点,分别把AB、BC、CD、DA分成1:2,得到一个小正方形A1B1C1D1,再用同样的方法在正方形A1B1C1D1内做正方形A2B2C2D2,…,这样无限的做下去,则所有这些正方形面积之和为 .
下列命题中不正确的是(其中l、m表示直线,α、β、γ表示平面)
| A.若l⊥m,l⊥α,m⊥β,则α⊥β |
| B.若α⊥γ,β∥γ,则α⊥β |
C.若l⊥m,l α,m α,m β,则α⊥β β,则α⊥β |
D.若l∥m,l⊥α,m β,则α⊥β β,则α⊥β |
一个调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出人数为
| A.5 |
| B.10 |
| C.25 |
| D.50 |
空间四边形ABCD中,AB=CD=3,E、F分别是BC、AD上的点,EF= ,
, ,则异面直线AB与CD所成角的大小为
,则异面直线AB与CD所成角的大小为
| A.30° | B.45° | C.60° | D.120° |
(本小题满分12分)
一个袋中装有大小相同,质量均匀的红球2个,白球3个,黑球3个,某人有放回的从袋中取球,每次取1个球,直到取得红球或取球5次时取球结束。
(Ⅰ)求第3次取球结束的概率;
(Ⅱ)求取球次数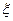 的分布列,并求出数学期望E
的分布列,并求出数学期望E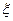 .
.
(本小题满分12分)
如图,在三棱锥P-ABC中,PA⊥平面ABC, ,PA =2, AB= AC=4,点D、E、F分别为BC、AB、AC的中点。
,PA =2, AB= AC=4,点D、E、F分别为BC、AB、AC的中点。
(I)求证:EF⊥平面PAD;
(II)求点A到平面PEF的距离.
(本小题满分12分)
如图所示,正三棱柱ABC—A1B1C1的底面边长是2,
侧棱长是,D是AC的中点.
(Ⅰ)求证:B1C//平面A1BD;
(Ⅱ)求二面角A—A1B—D的大小. 

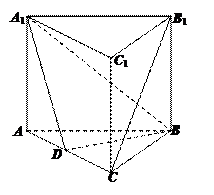
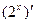 =__________.
=__________. = .
= .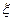 服从正态分布N(2,9),若P(
服从正态分布N(2,9),若P( __________.
__________. ,则
,则 = .
= . =
= ,且D
,且D =2,则D
=2,则D
 ,则
,则 等于
等于



 的分布列如右方表格,
的分布列如右方表格,
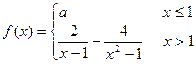 在x=1处连续,则
在x=1处连续,则 =
=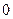
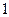
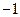
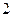
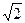 的正四棱锥S—ABCD内接于球O,则S、A两点的球面距离为
的正四棱锥S—ABCD内接于球O,则S、A两点的球面距离为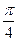
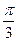
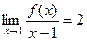 ,则f(1)=
,则f(1)=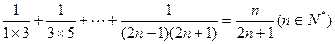
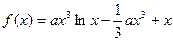
 处取得极值,求a的值;
处取得极值,求a的值; 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号