辽宁省锦州市高一第二学期期末考试数学试题
如图是在一次全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为
| A.84,4.84 | B.84,1.6 |
| C.85,1.6 | D.85,4 |
 |
人.现采用分层抽样取容量为45人的样本,那么高一、高二、高三年级抽取的人数分别为
| A.15,5,25 | B.15,15,15 | C.10,5,30 | D.15,10,20 |
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月 份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是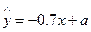 ,则
,则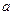 =
=
A.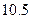 |
B. |
C.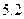 |
D.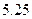 |
对于函数 ,下列命题:
,下列命题:
①函数图象关于直线 对称;
对称;
②函数图象关于点 对称;
对称;
③函数图象可看作是把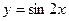 的图象向左平移个
的图象向左平移个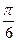 单位而得到;
单位而得到;
④函数图象可看作是把 的图象上所有点的横坐标缩短到原来的
的图象上所有点的横坐标缩短到原来的 倍(纵坐标不变)而得到;其中正确的命题是_________________.
倍(纵坐标不变)而得到;其中正确的命题是_________________.
某中学举行了一次“上海世博会知识竞赛”,从全校参加竞赛的学生的试卷中,随机抽取了一个样本,考察竞赛的成绩分布(得分均为整数,满分100分),将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.请结合直方图提供的信息,解答下列问题:
(Ⅰ)样本容量是多少?(Ⅱ)成绩落在那个范围内的人数最多?并求该小组的频数、频率;(Ⅲ)估计这次竞赛中,成绩高于60分的学生占总人数的百分比.
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为 .
.
(1)求直线 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.





 且点A坐标为
且点A坐标为 ,则点B的坐标为
,则点B的坐标为 




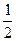 的是
的是 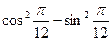
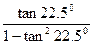



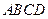 中,AB=5,BC=7,在其中任取一点P,使满足
中,AB=5,BC=7,在其中任取一点P,使满足 ,则P点出现的概率为
,则P点出现的概率为 

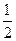
 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若 ,且当
,且当 时,
时,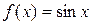 ,则
,则 的值为
的值为 

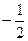


 的单调增区间为
的单调增区间为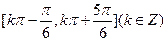
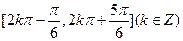
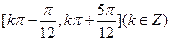
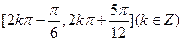
 ,且
,且 ,则实数
,则实数 = .
= . 的部分图像如下图所示:则函数
的部分图像如下图所示:则函数 的解析式为 .
的解析式为 .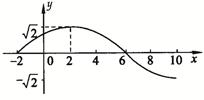

 之间的概率为 .
之间的概率为 . 是单位圆
是单位圆 上的点,且
上的点,且 是圆与
是圆与 轴正半轴的交点,
轴正半轴的交点,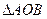 为正三角形. 若
为正三角形. 若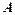 点的坐标为
点的坐标为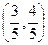 . 记
. 记 .
. 的值;
的值;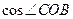 的值.
的值.
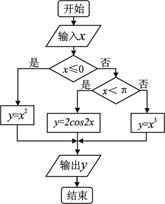
 ,向量
,向量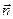 与向量
与向量 的夹角为
的夹角为 ,且
,且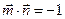 .
.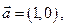 向量
向量 ,其中
,其中 ,若
,若 ,试求
,试求 的取值范围.
的取值范围.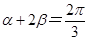 ,α和β为锐角.
,α和β为锐角.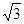 ,求β;
,求β; tanβ=2-
tanβ=2- 粤公网安备 44130202000953号
粤公网安备 44130202000953号