盐城市高三年级第三次调研考试数学试卷
9.由“若直角三角形两直角边的长分别为 ,将其补成一个矩形,则根据矩形的对角线长可求得该直角三角形外接圆的半径为
,将其补成一个矩形,则根据矩形的对角线长可求得该直角三角形外接圆的半径为 ”. 对于“若三棱锥三条侧棱两两垂直,侧棱长分别为
”. 对于“若三棱锥三条侧棱两两垂直,侧棱长分别为 ”,类比上述处理方法,可得该三棱锥的外接球半径为
”,类比上述处理方法,可得该三棱锥的外接球半径为 = ▲ .
= ▲ .
17.(本小题满分14分)
设数列 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
(Ⅰ)若 成等比数列,试求
成等比数列,试求 的值;
的值;
(Ⅱ)是否存在 ,使得数列
,使得数列 中存在某项
中存在某项 满足
满足 成等差数列?若存在,请指出符合题意的
成等差数列?若存在,请指出符合题意的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.


18.(本小题满分16分)
某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示. 其上部分是以 为直径的半圆,点
为直径的半圆,点 为圆心,下部分是以
为圆心,下部分是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 是两根支杆,其中
是两根支杆,其中 米,
米, . 现在弧
. 现在弧 、线段
、线段 与线段
与线段 上装彩灯,在弧
上装彩灯,在弧 、弧
、弧 、线段
、线段 与线段
与线段 上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为
上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为 ,节能灯的比例系数为
,节能灯的比例系数为 ,假定该霓虹灯整体的“心悦效果”
,假定该霓虹灯整体的“心悦效果” 是所有灯“心悦效果”的和.
是所有灯“心悦效果”的和.
(Ⅰ)试将 表示为
表示为 的函数;
的函数;
(Ⅱ)试确定当 取何值时,该霓虹灯整体的“心悦效果”最佳?
取何值时,该霓虹灯整体的“心悦效果”最佳?
19.(本小题满分16分)
已知椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,下顶点为
,下顶点为 ,点
,点 是椭圆上任一点,⊙
是椭圆上任一点,⊙ 是以
是以 为直径的圆.
为直径的圆.
(Ⅰ)当⊙ 的面积为
的面积为 时,求
时,求 所在直线的方程;
所在直线的方程;
(Ⅱ)当⊙ 与直线
与直线 相切时,求⊙
相切时,求⊙ 的方程;
的方程;
(Ⅲ)求证:⊙ 总与某个定圆相切.
总与某个定圆相切.
21.[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
A.(选修4—1:几何证明选讲)
如图,在梯形 中,
中, ∥BC,点
∥BC,点 ,
, 分别在边
分别在边 ,
, 上,设
上,设 与
与 相交于点
相交于点 ,若
,若 ,
, ,
, ,
, 四点共圆,求证:
四点共圆,求证: .
. 
22.(本小题满分10分)
已知动圆 过点
过点 且与直线
且与直线 相切.
相切.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作一条直线交轨迹
作一条直线交轨迹 于
于 两点,轨迹
两点,轨迹 在
在 两点处的切线相交于点
两点处的切线相交于点 ,
, 为线段
为线段 的中点,求证:
的中点,求证: 轴.
轴.
23.(本小题满分10分)
将一枚硬币连续抛掷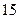 次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为
次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为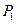 ,正面向上的次数为偶数的概率为
,正面向上的次数为偶数的概率为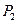 .
.
(Ⅰ)若该硬币均匀,试求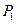 与
与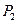 ;
;
(Ⅱ)若该硬币有暇疵,且每次正面向上的概率为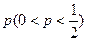 ,试比较
,试比较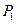 与
与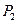 的大小.
的大小.
 ,则
,则 的虚部为 .
的虚部为 .  的
的 、
、 、
、 三所高校中,用分层抽样方法抽取
三所高校中,用分层抽样方法抽取 名志愿者,若在
名志愿者,若在 ▲ .
▲ . ”是假命题,则实数
”是假命题,则实数 的取值范围是 ▲ .
的取值范围是 ▲ . ,若
,若 ,则
,则 = ▲ .
= ▲ . ,若从
,若从 中任取一个元素作为直线
中任取一个元素作为直线 的倾斜角,则直线
的倾斜角,则直线 ,则
,则 的值为 ▲ .
的值为 ▲ . ▲ .
▲ .
 分别是椭圆
分别是椭圆 的上、下顶点和右焦点,直线
的上、下顶点和右焦点,直线 与椭圆的右准线交于点
与椭圆的右准线交于点 ,若直线
,若直线 ∥
∥ 轴,则该椭圆的离心率
轴,则该椭圆的离心率 = ▲ .
= ▲ . 满足
满足 ,则该数列的前20项的和为 ▲ .
,则该数列的前20项的和为 ▲ . 与圆
与圆 :
: 相交于
相交于 两点,若点M在圆
两点,若点M在圆 (
( 为坐标原点),则实数
为坐标原点),则实数 = ▲ .
= ▲ .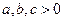 ,且
,且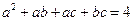 ,则
,则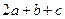 的最小值为 ▲ .
的最小值为 ▲ . ,函数
,函数 ,若对任意的
,若对任意的 ,都有
,都有 成立,则实数
成立,则实数 的取值范围为 ▲ .
的取值范围为 ▲ . 中,
中, ,
, 分别是
分别是 的中点.
的中点. 平面
平面 ;
; 平面
平面
 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
. 的大小;
的大小; ,试求
,试求 的最小值.
的最小值. .
. 有两个不同的解,求
有两个不同的解,求 的值;
的值; 时,不等式
时,不等式 恒成立,求
恒成立,求 在
在 上的最大值.
上的最大值. 成立的矩阵
成立的矩阵 .
. 与
与 ,它们相交于
,它们相交于 两点,求线段
两点,求线段 的长.
的长. 最大值.
最大值. 在等比数列
在等比数列 中,若
中,若 ,
, ,则
,则 ▲ .
▲ .  粤公网安备 44130202000953号
粤公网安备 44130202000953号