2013年初中数学单元提优测试卷-黄金分割点与平行线分线段成比例
如图,△ABC中,D为BC的中点,E为AC上任意一点,BE交AD于O.某同学在研究这一问题时,发现了如下事实:①当 =
= =
= 时,有
时,有 =
= =
= ;
;
②当 =
= =
= 时,有
时,有 =
= ;
;
③当 =
= =
= 时,有
时,有 =
= ;…;则当
;…;则当 =
= 时,
时, =( )
=( )
A. |
B. |
C. |
D. |
在平行四边形ABCD中,AC=4,BD=6,P是BD上的.任一点,过P作EF∥AC,与平行四边形的两条边分别交于点E,F.如图,设BP=x,EF=y,则能反映y与x之间关系的图象为( )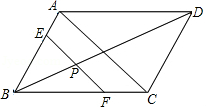
A.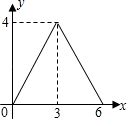 |
B.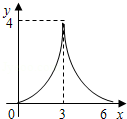 |
C.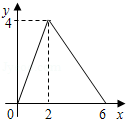 |
D.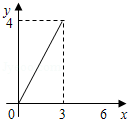 |
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是( )
A. |
B. |
C. ﹣1 ﹣1 |
D. +1 +1 |
如图,已知直线a∥b∥c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=6,BD=3,则BF=( )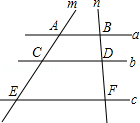
A.7 B.7.5 C.8 D.8.5
如图,△ABC是边长为6cm的等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积为( )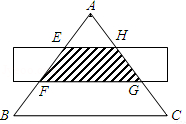
| A.4cm2 | B.2cm2 | C.3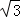 cm2 cm2 |
D.3cm2 |
已知线段AB及AB上一点P,当P满足下列哪一种关系时,P为AB的黄金分割点①AP2=AB•PB;②AP= AB;③PB=
AB;③PB= AB;④
AB;④ ;⑤
;⑤ .其中正确的是 (填“序号”)
.其中正确的是 (填“序号”)
如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,已知EF:DF=5:8,AC=24.
(1)求AB的长;
当AD=4,BE=1时,求CF的长.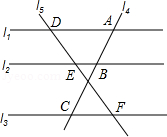
如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.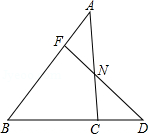
如图1,点C将线段AB分成两部分,如果 ,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
(2)研究小组在进一步探究中发现:过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.
如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即 ,BE交DC于点F,已知
,BE交DC于点F,已知 ,求CF的长.
,求CF的长.
如图,用纸折出黄金分割点:裁一张正方的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落到线段EA上,折出点B的新位置B′,因而EB′=EB.类似地,在AB上折出点B″使AB″=AB′.这时B″就是AB的黄金分割点.请你证明这个结论.
如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD与点O,某学生在研究这一问题时,发现了如下事实,
①当 ;
;
②当 ;
;
③ ;
;
如图4中,当 时,请你猜想
时,请你猜想 的一般结论,并证明你的结论(其中n为正整数).
的一般结论,并证明你的结论(其中n为正整数).
如图,AB∥EF∥CD,已知AC+BD=120,BC=50,EC+ED=96,求CF.
如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,DE=4,BC=6,AD=5.求DC与AE的长.
已知:▱ABCD中,E是BA边延长线上一点,CE交对角线DB于点G,交AD边于点F.
求证:CG2=GF•GE.
如图,在平行四边形ABCD中,点E为边BC上一点,连接AE并延长AE交DC的延长线于点M,交BD于点G,过点G作GF∥BC交DC于点F.
求证: .
.
如图,已知△ABC中,DE∥BC交AB于点D,交AC于点E,点M在BC边上,AM交DE于点F.
求证: .
.

 = .
= . = ;
= ;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号