[重庆]2013届重庆市万州区岩口复兴学校九年级下学期第一次(3月)月考数学卷
观察下列“风车”的平面图案,其中既是轴对称又是中心对称图形的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下列调查中,适合采用全面调查(普查)方式的是( )
| A.对某班50名同学视力情况的调查 | B.对元宵节期间市场上汤圆质量情况的调查 |
| C.对某类烟花爆竹燃放质量情况的调查 | D.对长江水质情况的调查 |
如图,在△ABC中,∠C=90°,若BD∥AE,∠DBC=20°,则∠CAE的度数是( )
| A.40° | B.60° | C.70° | D.80° |
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )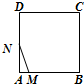
A.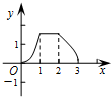 |
B.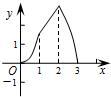 |
C.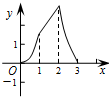 |
D.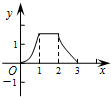 |
下列图形都是由同样大小的正方形和正三角形按一定的规律组成,其中,第①个图形中一共有5个正多边形,第②个图形中一共有13个正多边形,第③个图形中一共有26个正多边形,……,则第⑥个图形中正多边形的个数为( )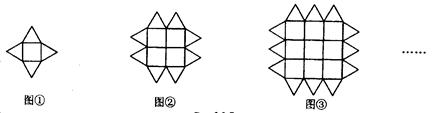
| A.90 | B.91 | C.115 | D.116 |
已知:抛物线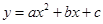 (
(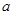 ≠
≠ )在平面直角坐标系的位置如图所示,则下列结论中正确的是( )
)在平面直角坐标系的位置如图所示,则下列结论中正确的是( )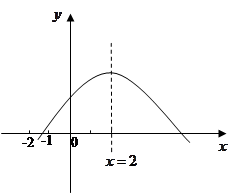
A.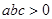 |
B.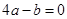 |
C.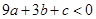 |
D.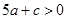 |
2012年我市积极引进海外投资,到今年五月初,引入的总投资已达到3120000万元,则数据3120000用科学记数法表示为 .
为了解初三学生的视力情况,某校随机抽取50名学生进行视力检查,结果如下:
| 视力 |
4.6以下 |
4.6 |
4.7 |
4.8 |
4.9 |
5.0 |
5.0以上 |
| 人数(人) |
6 |
15 |
5 |
10 |
3 |
4 |
7 |
这组数据的众数与中位数的和是 。
已知关于x的方程(a+2)x2-3x+ 1=0,如果从-2,-1,0,1,2五个数中任取一个数作为此方程的a,那么所得方程有实数根的概率是
万达广场有一部自动扶梯匀速由下而上运动,甲、乙两人在乘扶梯的同时匀速登梯,甲登了30级后到达楼上,乙登梯的速度是甲的2倍(单位时间内乙登楼级数是甲的2倍),他登了36级后到达楼上,那么由楼下到楼上自动扶梯级数为 .
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,求线段DF的长.
如图,在平面直角坐标系中,点 是反比例函数
是反比例函数
 图象上一点,
图象上一点, ⊥
⊥ 轴于
轴于 点,一次函数
点,一次函数
 的图象交
的图象交 轴于
轴于 ,交
,交 轴于
轴于 点,并与反比例函数的图象交于
点,并与反比例函数的图象交于 两点,连接
两点,连接 若△
若△ 的面积为4,且
的面积为4,且 .
.
(1) 分别求出该反比例函数和一次函数的解析式;
(2) 求△ 的面积.
的面积.
在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图。 1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有_________名学生。
1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有_________名学生。
2)补全女生等级评定的折线统计图。
3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率。
在 中,对角线
中,对角线 为BD延长线上一点且
为BD延长线上一点且 为等边三角形,
为等边三角形, 、
、 的平分线相交于点
的平分线相交于点 ,连接
,连接 ,连接
,连接 。
。
(1)若 的面积为
的面积为 ,求
,求 的长;
的长;
(2)求证: 。
。
重庆市某房地产开发公司在2012年2月以来销售商品房时,市场营销部经分析发现:随着国家政策调控措施的持续影响,大多市民持币观望态度浓厚,从2月起第1周到第五周,房价y1(百元/m²)与周数x(1≤x≤5,且x取正整数)之间存在如图所示的变化趋势:3月中旬由于房屋刚性需求的释放,出现房地产市场“小阳春”行情,房价逆市上扬,从第6周到第12周,房价y2与周数x(6≤x≤12,且x取整数)之间关系如下表:
| 周数x |
6 |
7 |
9 |
10 |
12 |
房价 (百元/m²) (百元/m²) |
68 |
69 |
71 |
72 |
74 |
(1)根据如图所示的变化趋势,直接写出 与x之间满足的函数关系式;请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出
与x之间满足的函数关系式;请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出 与x之间的函数关系式,
与x之间的函数关系式,

(2)已知楼盘的造价为每平米30百元,该楼盘在1至5周的销售量p1(百平方米)与周数x满足函数关系式p1=x+74(1≤x≤5,且x为整数),6至12周的销售量p2(百平方米)与周数x满足函数关系式p2=2x+80(6≤x≤12,且x取整数),试求今年1至12周中哪个周销售利润最大,最大为多少万元?
(3)市场营销部分析预测:从五月开始,楼市成交均价将正常回落,五月(以四个周计算)每周的房价均比第12周下降了 %,楼盘的造价不变,每周的平均销量将比第12周增加5
%,楼盘的造价不变,每周的平均销量将比第12周增加5 %,这样以来5月份将完成总利润20800万元的销售任务,请你根据参考数据,估算出
%,这样以来5月份将完成总利润20800万元的销售任务,请你根据参考数据,估算出 的最小整数值。
的最小整数值。
(参考数据: ,
, ,
, ,
, )
)
如图 ,梯形
,梯形 中,
中, ∥
∥ ,
, ,
, ,
, .动点
.动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度在线段
个单位长度的速度在线段 上运动;动点
上运动;动点 同时从点
同时从点 出发,以每秒
出发,以每秒 个单位长度的速度在线段
个单位长度的速度在线段 上运动.以
上运动.以 为边作等边△
为边作等边△ ,与梯形
,与梯形 在线段
在线段 的同侧.设点
的同侧.设点 、
、 运动时间为
运动时间为 ,当点
,当点 到达
到达 点时,运动结束.
点时,运动结束.
(1)当等边△ 的边
的边 恰好经过点
恰好经过点 时,求运动时间
时,求运动时间 的值;
的值;
(2)在整个运动过程中,设等边△ 与梯形
与梯形 的重合部分面积为
的重合部分面积为 ,请直接写
,请直接写
出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;
(3)如图 ,当点
,当点 到达
到达 点时,将等边△
点时,将等边△ 绕点
绕点 旋转
旋转 (
( ),
),
直线 分别与直线
分别与直线 、直线
、直线 交于点
交于点 、
、 .是否存在这样的
.是否存在这样的 ,使△
,使△ 为等腰三角形?
为等腰三角形?
若存在,请求出此时线段 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
 ,
, ,1,2这四个数中,最小的数是
,1,2这四个数中,最小的数是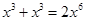
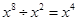
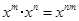
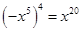
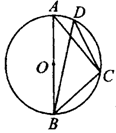
 的直径,点
的直径,点 、
、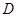 都在
都在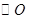 上,若
上,若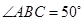 ,则
,则 ( )
( )
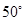
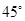
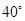
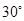
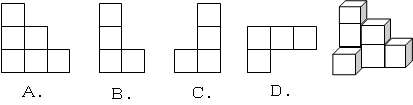
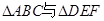 相似且对应高线的比为
相似且对应高线的比为 ,则
,则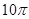 ,半径为6,则该扇形的圆心角度数为______________.
,半径为6,则该扇形的圆心角度数为______________.
 。
。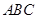 中,∠
中,∠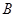 =30°,
=30°,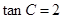 ,
,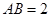 ,求△
,求△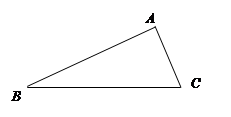
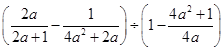 ,其中
,其中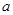 是不等式
是不等式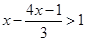 的最大整数解。
的最大整数解。 粤公网安备 44130202000953号
粤公网安备 44130202000953号