北京市东城北区初二上学期期末考试数学卷
如图,已知在平行四边形 中,
中, ,
, ,
, .
.
(1)用 、
、 表示
表示 、
、 ;(直接写出答案)
;(直接写出答案)
(2)求作 分别在
分别在 、
、 方向上的分向量.
方向上的分向量.
(不要求写作法,但要指出图中表示结论的向量)
如图,一块梯形木料 ,
, ∥
∥ ,经测量知
,经测量知 cm,
cm, cm,
cm, ,
, ,求梯形木料
,求梯形木料 的高.
的高.
(备用数据 :sin 67.4° = ,cos 67.4° = ,tan 67.4° = )
:sin 67.4° = ,cos 67.4° = ,tan 67.4° = )
已知抛物线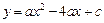 与
与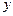 轴交于点
轴交于点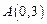 ,点
,点 是抛物线上的点,且满足
是抛物线上的点,且满足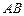 ∥
∥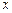 轴,点
轴,点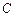 是抛物线的顶点.
是抛物线的顶点.
(1)求抛物线的对称轴及 点坐标;
点坐标;
(2)若抛物线经过点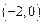 ,求抛物线的表达式;
,求抛物线的表达式;
(3)对(2)中的抛物线,点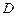 在线段
在线段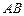 上,若以点
上,若以点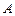 、
、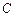 、
、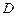 为顶点的三角形与
为顶点的三角形与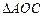 相似,试求点
相似,试求点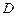 的坐标.
的坐标.
如图,已知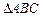 与
与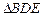 都是等边三角形,点
都是等边三角形,点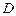 在边
在边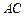 上(不与
上(不与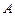 、
、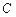 重合),
重合),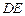 与
与 相交于点
相交于点 .
.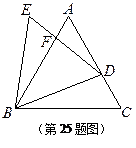
(1)求证:
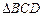 ∽
∽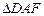 ;
;
(2)若 ,设
,设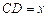 ,
,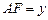 ;
;
①求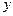 关于
关于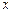
 的函数解析式及定义域;
的函数解析式及定义域;
②当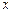 为何值时,
为何值时,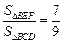 ?
?
根据下列表述,能确定位置的是 ( )
| A.某电影院2排 | B.汉中市大桥南路 |
| C.北偏东30° | D.东经118°,北纬40° |
下列函数中,y的值随x的值增大而增大的是( )
| A.y= -3x | B.y="2x" - 1 | C.y= -3x+10 | D.y= -2x+1 |
直线y="k" x+b经过一、二、四象限,则k、b应满足 ( )
| A. k>0, b<0 | B. k>0,b>0 | C. k<0, b<0 | D.k<0, b>0 |
根据下列一次函数y =" kx" + b的图象,常数k、b的符号正确的是( ).
| A.k﹥0,b﹤0 | B.k﹤0,b﹥0 | C.k﹤0,b﹤0 | D.k﹤0,b﹥0 |
一次函数y =" -2x" -3不经过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
四边形:平行四边形、矩形、菱形、正方形、等腰梯形中,对角线相等的有 ( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h (厘米)与燃烧时间t (时)的函数关系的图象是( )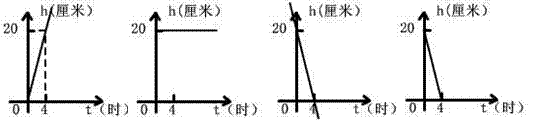
A B C D
甲、乙两人同时沿着一条笔直的公路朝同一方向前行,开始时,乙在甲前2千米处,甲、乙两人行走的路程S(千米)与时间 (时)的函数图象(如图所示),下列说法正确的是( )
(时)的函数图象(如图所示),下列说法正确的是( )
| A.乙的速度为4千米/时 |
| B.经过1小时,甲追上乙 |
| C.经过0.5小时,乙行走的路程约为2千米 |
| D.经过1.5小时,乙在甲的前面 |
已知关于x的一次函数y =" mx" + 4m-2的图象经过原点,那么m = ;若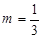 ,则这个函数的图象经过第 象限;若
,则这个函数的图象经过第 象限;若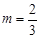 ,则这个函数的图象经过第 象限.
,则这个函数的图象经过第 象限.
点M(3,-3)关于y轴对称的点的坐标是
| A.(3,–3) | B.(3,3) | C.(–3,3) | D.(–3,–3) |
等腰三角形的一个角是80°,则它的底角是
| A.50° | B. 80° | C. 50°或80° | D. 20°或80° |
将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是 
如图所示,在长方形ABCD的对称轴l上找点P,使得△PAB、△PBC均为等腰三角形,则满足条件的点P有
A.1个 B.3个 C.5个 D.无数多个
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于__________

.
如图,等边△ABC的边长为2cm,D,E分别是A B,AC上的点,将△ADE沿直线DE折叠,点A落在点
B,AC上的点,将△ADE沿直线DE折叠,点A落在点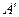 处,且点
处,且点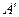 在△AB
在△AB C外部,则阴影部分图形的周长为 cm
C外部,则阴影部分图形的周长为 cm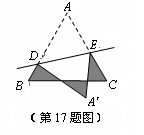
已知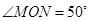 ,点P为
,点P为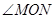 内一点,点A为OM上一点,点B为ON上一点,当
内一点,点A为OM上一点,点B为ON上一点,当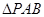 的周长取最小值时,
的周长取最小值时, 的度数为_______________.
的度数为_______________.
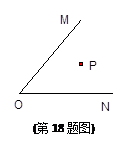
如图,直线l1的函数解析式为y=x+1,且l1与x轴交于点D,直线l2经过定点A,B,直线l1与l2交于点C.
(1)求直线l2的函数解析式;
(2)求△ADC的面积.
某工厂,加负责加工A型零件,乙负责加工B型零件。已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,每天甲、乙两人共加工两种零件35个,设甲每天加工 个A型零件.
个A型零件.
(1)求甲、乙每天各加工多少个零件;(列分式方程 解应用题)
解应用题)
(2)根据市场预测估计,加工A型零件所获得的利润为m元/ 件(3≤m≤5) ,加工B型零件所获得的利润每件比A型少1元.求每天甲、乙加工的零件所获得的总利润
,加工B型零件所获得的利润每件比A型少1元.求每天甲、乙加工的零件所获得的总利润 (元)与m(元/件)的函数关系式,并求总利润
(元)与m(元/件)的函数关系式,并求总利润 的最大值、最小值.
的最大值、最小值.
如图1,在矩形ABCD中,AB=12厘米,BC=6厘米,点P从A点出发,沿A →B→C→D路线运动,到D点停止;点Q从D点出发,沿D →C →B →A运动,到A点停止.若点P,点Q同时出发,点P的速度为每秒1厘米,点Q的速度为每秒2厘米,a秒时点P ,点Q同时改变速度,点P的速度变为每秒b厘米,点Q的速度变为每秒c厘米.如图2是描述点P出发x秒后△APD
,点Q同时改变速度,点P的速度变为每秒b厘米,点Q的速度变为每秒c厘米.如图2是描述点P出发x秒后△APD 的面积S1(
的面积S1( )与x(秒)的函数关系的图象.图3是描述点Q出发x秒后△AQD的面积S2(
)与x(秒)的函数关系的图象.图3是描述点Q出发x秒后△AQD的面积S2( )与x(秒)的函数关系图象.根据图象:
)与x(秒)的函数关系图象.根据图象: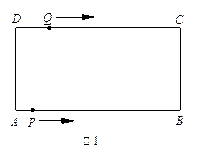
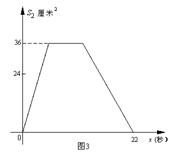
(1)求a、b、c的值;
(2)设点P离开点A的路程为y1(厘米),点Q到点A还需要走的路程为y2(厘米 ),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式,并求出P与Q相遇时x的值.
),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式,并求出P与Q相遇时x的值.
 中,
中, ,如果
,如果 ,
, ,那么
,那么
 、
、 分别是
分别是 的边
的边 、
、 上的点,
上的点, ,
, ,
, ,如果要使
,如果要使 ∥
∥ ,则
,则
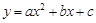 与
与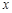 轴交于点
轴交于点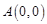 、
、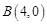 ,则抛物线的对称轴为直线
,则抛物线的对称轴为直线 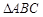 中,
中, ,
,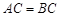 ,若点
,若点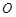 是
是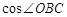 =_______
=_______ 沿直线
沿直线 翻折,使点
翻折,使点 与
与 边上的点
边上的点 重合,若
重合,若 ,
, ,则
,则

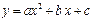 经过点(–5,0)、(–1,0)、(1,12),求这个抛物线的表达式及其顶点坐标
经过点(–5,0)、(–1,0)、(1,12),求这个抛物线的表达式及其顶点坐标 中,
中, ,点
,点 在
在 上,
上, ,
, ,
,  ,求
,求 的长.
的长.
 中,
中, 与
与 相交于点
相交于点 ,AB⊥AC,CD⊥BD.
,AB⊥AC,CD⊥BD.
 ∽
∽ ;
; ,
, ,求
,求 的值
的值 时,自变量 x的范围是( )
时,自变量 x的范围是( )




 的解是( )
的解是( )



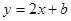 的图象经过点A(—1,1)则b=
的图象经过点A(—1,1)则b= 



 有意义,
有意义, 必须满足的条件是
必须满足的条件是



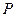 表示的数可能是
表示的数可能是 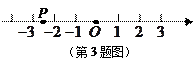
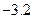
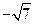

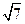
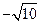
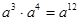
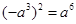
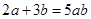
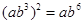
 ,
, ,
, ,
, ,
, ,其中无理数有
,其中无理数有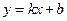 交坐标轴于
交坐标轴于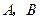 两点,则关于
两点,则关于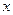 的不等式
的不等式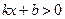 的解集是
的解集是
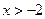
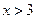
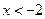
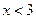
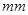 ,用科学记数法表示是
,用科学记数法表示是 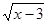 的自变量
的自变量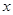 的取值范围是
的取值范围是 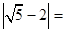 _____________
_____________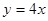 向上平移2个单位,所得直线表达式是______
向上平移2个单位,所得直线表达式是______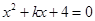 是一个完全平方式,则
是一个完全平方式,则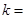 _________
_________ ; (2)
; (2)
 ;
;  .
.
 ,其中
,其中
 ,点
,点 是
是 的交点,点
的交点,点 是
是 的中点.试判断
的中点.试判断 和
和
 粤公网安备 44130202000953号
粤公网安备 44130202000953号