[江苏]2012-2013学年江苏苏州八年级上期中检测数学试卷
实数:-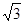 ,π,0.27,
,π,0.27,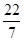 ,
,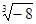 ,
,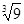 ,0.3,0.1010010001…,有理数的个数是
,0.3,0.1010010001…,有理数的个数是
| A.3 | B.4 | C.5 | D.6 |
如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为 
| A.50° | B.30° | C.100° | D.90° |
我国以2011年11月1日零时为标准记时点,进行了第六次全国人口普查,查得全国总人口约为1 370 000 000人,请将总人口数用科学计数法表示为
A. |
B. |
C. |
D. |
如图,△ABC中,BI、CI分别平分∠ABC、∠ACF,DE过点I,且DE∥BC,BD=8cm,CE=5cm,则DE等于
A.2cm
B.3cm
C.4cm
D.5cm
下列给出的条件中,能判定四边形ABCD为平行四边形的是
A.AB=CD,CD=DA;
B.AB∥CD,AD=BC;
C.AB∥CD,∠A=∠C;
D.∠A=∠B,∠C=∠D.
如图,在梯形ABCD中,AD∥BC,AB=AD,BD=BC,∠A=100°,则∠BDC的度数为
| A.60° | B.65° | C.70° | D.75° |
若等腰三角形的一个内角等于50°,则另外两个角的度数分别为
| A.50°、80° | B.65°,65° |
| C.50°、65°或 65°,80° | D.50°、80或 65°,65° |
下列说法正确的是
| A.有理数与数轴上的点一一对应 |
| B.对角线相等的梯形是等腰梯形 |
| C.直角三形的两边长是5和12,则第三边长是13 |
| D.近似数1.5万精确到十分位 |
如图,矩形纸片ABCD,AD=BC=3,AB=CD=9,在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK,则对△MNK的叙述正确的个数是:①△MNK一定是等腰三角形;②△MNK可能是钝角三角形;③△MNK有最小面积且等于4.5;④△MNK有最大面积且等于7.5
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,矩形OABC的边OA长为2 ,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴上原点右边于一点,则这个点表示的实数是________.
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为 .
如图,分别以△ABC的三边为边向外作3个正方形,面积分别为1,2,3,则此△ABC________(填“是”,“不是”) 直角三角形.
如图,一块等腰直角的三角板ABC, 在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,若A,C, B′三点在同一直线上,则旋转角度的大小为 度.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为_____cm .
.
我们已学会了用“两边夹”的方法,根据不同的精确度要求,估算 的取值范围,我们还可以用“逼近”的方法,求出它的近似值.
的取值范围,我们还可以用“逼近”的方法,求出它的近似值.
| x |
1.40 |
1.41 |
1.42 |
1.43 |
… |
| x2 |
1.96 |
1.9881 |
2.0164 |
2.0449 |
… |
2-1.9881=0.0119,2.0164-2=0.0164,0.0119<0.0164
可见1.9881比2.0164更逼近2,当精确度为0.01时, 的近似值为1.41.
的近似值为1.41.
下面,我们用同样的方法估计方程x2+2x=6其中一个解的近似值.
| x |
1.63 |
1.64 |
1.65 |
1.66 |
… |
| x2+2x |
5.9169 |
5.9696 |
6.0225 |
6.0756 |
… |
根据上表,方程x2+2x=6的一个解约是______________.(精确到0.01)
如图,矩形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为__________
木工师傅为了让直尺经久耐用,常常在直尺的直角顶点与斜边之间加一根小木条,如下左图所示.下右图为其示意图.若∠BAC=90°,线段AB的长为15cm,线段AC的长为20cm,试求出小木条AD的最短长度.
如图,正方形网格中,小格的顶点叫做格点,连接任意两个格点的线段叫做格点线段。
(1)如图1,格点线段AB、CD,请添加一条格点线段EF,使它们构成轴对称图形;
(2)如图2,格点线段AB和格点C,在网格中找一格点D,使格点A、B、C、D四点构成中心对称图形;
(3)在(2)的条件下,如果每一小正方形边长为1,那么四边形ABCD的面积S为_________.
(请直接填写)
如图,等边三角形ABC,点E是AB上一点,点D在CB的延长线上,且ED=EC,
EF∥AC交BC于点F.
(1)试说明四边形AEFC是等腰梯形;
(2)请判断AE与DB的数量关系,并说明你的理由.
已知:如图,在 中,
中, 是
是 边的中点,
边的中点, 是
是 的中点,连接
的中点,连接 并延长到点
并延长到点 ,使EF=BE,连结AF、
,使EF=BE,连结AF、 .
.
(1)试说明ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形 是矩形,并说明你的理由.
是矩形,并说明你的理由.
如图: 在梯形ABCD中,AB∥DC,AD=DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB,垂足为F.
(1) 写出图中相等的线段; (已知的相等线段除外)
(2) 若AD=5,CF=4,求四边形ABCD的面积.


 )0+ (
)0+ ( )-1-
)-1- -|3-π|
-|3-π| (2)3(x-1)3+24=0
(2)3(x-1)3+24=0
 自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形BPDQ是平行四边形时,求m与n满足的数量关系.(画出示意图)
自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形BPDQ是平行四边形时,求m与n满足的数量关系.(画出示意图) 粤公网安备 44130202000953号
粤公网安备 44130202000953号