[浙江]2012-2013学年浙江温州育英学校八年级10月月考数学试卷1
关于 的二次函数
的二次函数 ,下列说法正确的是( )
,下列说法正确的是( )
| A.图象的开口向上 | B.图象与 轴的交点坐标为(0,2) 轴的交点坐标为(0,2) |
| C.图象的顶点坐标是(-1,2) | D.当 时, 时, 随 随 的增大而减小 的增大而减小 |
下列命题中,正确的是( )
①平分弦的直径垂直于弦;②圆内接平行四边形必为矩形;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤相等的圆周角所对的弧相等.
| A.①②③ | B.②③④ | C.②③④⑤ | D.①②③④⑤ |
已知弦AB把圆周分成1:5的两部分,则弦AB所对应的圆心角的度数为( )。
| A.60° | B.30°或150° | C.30° | D.60°或300° |
矩形ABCD中,AB=8, 点P在边AB上,且BP=3AP,如果圆P是以点P点为圆心,PD为半径的圆,那么下列判断正确的是( )
点P在边AB上,且BP=3AP,如果圆P是以点P点为圆心,PD为半径的圆,那么下列判断正确的是( )
A.点B、C均在圆P外 B.点B在圆P内、点C在圆P外
C.点B、C均在圆P内 D.点B在圆P外、点C在圆P内
如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,
 ,则
,则 的度数为( )
的度数为( ) 
二次函数y=ax2+bx+c(a≠0)的图象所示,若∣ax2+bx+c∣=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
| A.k<-3 | B.k>-3 | C.k<3 | D.k>3 |

在测量某物理量的过程中,因为仪器和观察的误差,使得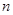 次测量分别得到
次测量分别得到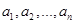 共
共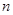 个数据,我们规定所测得的物理量的“最佳近似值”
个数据,我们规定所测得的物理量的“最佳近似值”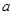 是这样一个数据:与其他近似值比较,
是这样一个数据:与其他近似值比较,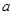 与各个数据差的平方和最小。若三次测量得到的数据依次为
与各个数据差的平方和最小。若三次测量得到的数据依次为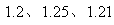 ,依据此规定,那么本次测量的“最佳近似值”为( )
,依据此规定,那么本次测量的“最佳近似值”为( )
定义符号 表示与自变量
表示与自变量 所对应的函数值。例如对于函数
所对应的函数值。例如对于函数 ,当
,当 时,对应的函数值
时,对应的函数值 ,则可以写为:
,则可以写为: 。在二次函数
。在二次函数 中,若
中,若 对任意实数
对任意实数 都成立,那么下列结论错误的是( )
都成立,那么下列结论错误的是( )
函数 的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3);②当
的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3);②当 ;④当
;④当 逐渐增大时,
逐渐增大时, 随着x的增大而减小.其中正确结论的序号是____ _.
随着x的增大而减小.其中正确结论的序号是____ _.
如图,把抛物线 平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线
平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线 交于点Q,则图中阴影部分的面积为________________.
交于点Q,则图中阴影部分的面积为________________.
如图,已知点P是反比例函数 图象上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数
图象上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数 图象于E、F两点. 用含k1、k2的式子表示四边形PEOF的面积为 ;
图象于E、F两点. 用含k1、k2的式子表示四边形PEOF的面积为 ;
已知二次函数 的顶点为A,与y轴交于点B,作它关于以P(1,0)为中心的中心对称的图像顶点为C,交y轴于点D,则四边形ABCD面积为________.
的顶点为A,与y轴交于点B,作它关于以P(1,0)为中心的中心对称的图像顶点为C,交y轴于点D,则四边形ABCD面积为________.
已知点A、B分别是 轴、
轴、 轴上的动点,点C、D是某函数图像上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。如图,正方形ABCD是反比例函数
轴上的动点,点C、D是某函数图像上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。如图,正方形ABCD是反比例函数 图像上的其中一个伴侣正方形。则这个伴侣正方形的边长是____________;
图像上的其中一个伴侣正方形。则这个伴侣正方形的边长是____________;
(1)将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2= ;
(2)如图,P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于
|
点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,则所有满足条件的t的值为 .

自变量为x的二次函数
(1) ,求函数值y的最大值与最小值;并分别指出所对应的自变量x的值;
,求函数值y的最大值与最小值;并分别指出所对应的自变量x的值;
(2)当a变化时,该二次函数图象是否经过定点?若是,请求出定点坐标;若不是,请说明理由;
(3)若该二次函数图象与x轴有两个不同的交点,而且两交点的横坐标均小于-1,求a的取值范围。
阅读下面的情境对话,然后解答问题
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
1求证: ACE是奇异三角形;
ACE是奇异三角形;
2当 ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
有一种产品的质量分成6种不同档次,若工时不变,每天可生产最低档次的产品40件;如果每提高一个档次,每件利润可增加1元,但每天要少生产2件产品。
⑴若最低档次的产品每件利润17元时,生产哪一种档次的产品的利润最大?并求最大利润。
⑵由于市场价格浮动,生产最低档次的产品每件利润可以从8元到24元不等,那么生产哪种档次的产品所得利润最大?
 都在反比例函数
都在反比例函数 的图象上,若
的图象上,若 ,则下列式子正确的是( )
,则下列式子正确的是( )
 的图像先向左平移1个单位,再向上平移一个单位后所得函数解析式为( )
的图像先向左平移1个单位,再向上平移一个单位后所得函数解析式为( )
 的顶点在坐标轴上,则k= .
的顶点在坐标轴上,则k= . (a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程
(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程 的解为 .
的解为 . 为直线
为直线 上的两点,过
上的两点,过

 恒成立,那么实数x的取值范围是
恒成立,那么实数x的取值范围是 
 粤公网安备 44130202000953号
粤公网安备 44130202000953号